Numbers and their uses
Chapter 2 - Understanding Numbers
Section 2.2 - Interpreting Numbers
Two times zero is still zero and half of infinity is still
infinity.
If you
want to develop good engineering judgment you
need to understand the profound meaning of this perspective on zero and
infinity. When dealing with very small
numbers, it makes no difference in the greater scheme of things whether
the number is doubled or not. The number will
still be a small number and needs to be interpreted that way.
Similarly
when dealing with large numbers, even if you halve
the number you still are left with a large number. For all numbers in
between you can use relative comparisons , however,
for small and large numbers, one needs to understand that relative
comparisons may not hold true.
You are probably confused as to what defines a really large and small
number. Relative does not have any absolute number interpretation.
Relative comparison only has meaning in relation to what you are comparing
to. You have to use engineering judgment to see what range most
numbers fall within.
For example, a transportation engineer measuring average
traffic flow on a highway will see most speeds fall within 45-65 mph.
The engineer only needs to focus on speeds in that range
and ignore the really small speeds close to zero. The slowest car in one highway may be 30 mph and in
another highway could be 10 mph. This does not mean the first highway has a 300% higher average
speed of slow cars. It means both those speeds are well below the average speed and
cannot be compared to each other. The example next will explain this in more detail.
Consider an engineer who is given a half-sphere of material and is
asked to build a stool from it that will be supported at three points.
The engineer needs to find the optimal load path to support a person
sitting on the top of the sphere and supported at three points
equidistant apart at the base. This type of analysis is called
'Topology Optimization' and requires building a virtual model on the
computer and uses equations of calculus and material science to solve a
computationally intensive simulation on a supercomputer.
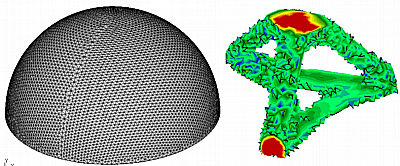
The picture above on the right is called the 'Optimal load path' .
The way to interpret it is areas in red indicate areas of highest
stress, so need material there. Areas in green are also under stress,
while areas in blue have almost no stress. Actually most of the sphere
is blue, however, all the blue parts of the model were taken out of the
sphere so you could see the internal green and red parts of the model.
Before continuing, it will be useful to understand what
stress means. Stress is an engineering concept and is simply the
load or force divided by the area over which it is applied. Materials
fail when the internal stress from external loads exceeds their allowable
yield stress. Materials like steel have a high yield stress while those
like
rubber have a low yield stress.
Think of this as a pin pricking you. A pin with a sharp point will
be a lot more painful than a pin with a blunt point. The reason is the
same
load is going through a small area, thereby increasing the stress you
feel.
Now suppose the same problem of designing the stool
were given to another engineer. This engineer will
use a different software and methodology to build his virtual model.
In areas where the sphere is taking no load, the results from
both engineer's model should be blue
or the stress should theoretically be close to zero. However one engineer
says the stress in the blue area is 1 MPa, while the other says
it is 2 MPa ( MPa is a measure of force per unit area ). Does this mean the second engineer is producing results
with 50% error ? No , it means both engineer's analysis are outputting
very small
numbers which are close to zero and therefore the SAME number.
Now consider you are looking at load near one of the three support points
at the base. Theoretical results say the stress from load should be
infinity as you have a high load going through an infinitely small
point. Now one engineer says it is 6000 MPa, while
the other engineer's analysis shows 3000 MPa. Again does this mean
the results have 50%
error? No, it means both engineer's analysis
are outputting very large numbers which correlate to the trend of
infinite stress and are therefore the SAME number.
Too many engineers only focus on the absolute numbers when comparing
analysis results. Good engineering judgment involves looking at relative
differences and also seeing how large or small the numbers are when
making comparisons. Another way of thinking of this is in terms of
order of magnitude. Small or very large numbers within the same order
of magnitude are essentially the same number for all practical
purposes. This is not only true in science but all life in general.
It is important to understand the concept of interpreting numbers as
even many engineers with PhD's do not get it. Often those in the
scientific community are too focused on the absolute details and fail to
see the bigger picture around them.
Another problem scientists have is
reporting results with too many significant digits. For example an
atmospheric
scientist
who says the temperature is 97.6756 Farenheit or 22.22323 Celsius is
only confusing you by adding so many significant digits. They may be more
'accurate', however by increasing confusion they defeat the purpose behind
reporting
the number! Only report just enough digits that are truly
significant. So one should report temperature to within 1 whole degree as
few people
can perceive differences of a tenth of a degree.
Of course there are many situations where modeling the absolute
response is of critical importance. It takes good engineering judgment
to know when one needs to look at absolute numbers and when one needs to
only look at relative differences in numbers. You are now in a much
better position to interpret numbers now that you understand
how relative comparisons work for large and small numbers.
Next section ->
Section 2.3 - Risk Assessment