CHAPTER 3
Chapter 3 - The Mathematical function and its Graph
Section 3.5 - Two dimensional functions
Calculus is about analyzing functions that change. Until now it has been assumed that all the independent dimensions in an n-dimensional functions are constant and remain fixed. It is not difficult to see how changes in an independent dimension give rise to changes in the dependent dimension. For example if the mass of an object doubles, the force to push it at the same acceleration will also double.
Allowing more than one dimension to change poses a challenge that is the focus of an advanced course, multi-variable Calculus. The scope of this text will be limited to n-dimensional functions in which only one dimension is allowed to change. The n-dimensional functions thus reduces to two dimensions, in which a change in the independent dimension produces a proportional change in the dependent dimension.
Before explaining what is meant by a changing dimension, let us see how functions of several dimensions can be reduced to simple two dimensional functions. Consider the four dimensional function for the attractive force ( gravity ) between two bodies of different masses separated by a certain distance from each other. The force of attraction is given by Newton’s Law of Gravitation:
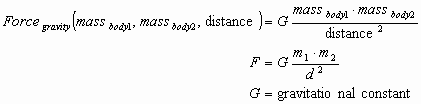
IF we were given the masses of two bodies and the distance separating them, then the force of attraction would be a simple matter of plug and chug. Suppose we were only given the mass of one object as 1000 kg, and the distance between it and object 2 to be equal to 1,000,000 meters. The function would reduce to:
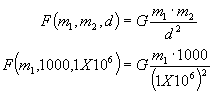
The fixed independent dimensions give rise to a constant that can be separated from the function such that:
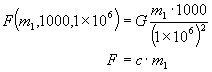
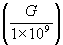was replaced by a constant c. The gravitation force is now only a function of the first object mass, since all other conditions are given. Thus:
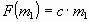
The force depends on whatever the mass we choose to enter multiplied by some constant that is dependent on the situation already known. Thus we have reduced a four dimensional function to two dimensions by entering conditions that are already known. Therefore, any n-dimensional function can be reduced to two dimensions, provided ( n-2 ) dimensions are already given/
Questions
1) Play with the gas savings calculator and try and derive the equations used
2) The amount of interest earned by money in a savings account is given by the function:
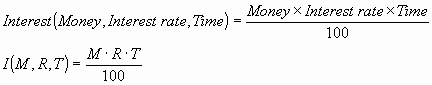
Or simply:
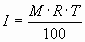
- Given a deposit of $1000 and an interest rate of 6 %, write a two dimensional function of interest earned as a function of time
- Find the interest earned after 2, 3 and 10 years
