CHAPTER 5
Chapter 5 - Differentiating Functions
Section 5.5 - Differentiating Functions of Functions
The last technique of
differentiation is for differentiating functions of functions of x or functions of the form,
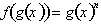. For example consider the function:
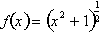
The derivative is not
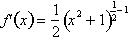because we also need
to take into consideration the inside function of x,
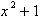. We can replace
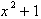with g(x) and get:
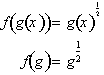
To find the derivative of
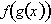with respect to x, we first need to find the derivative
of f with respect to g. From the definition of the
derivative:
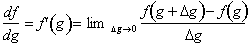
Next we find the
derivative of g(x), the inside
function, with respect to x.
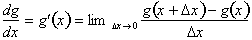
Now we multiply the two derivatives
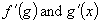to get df / dx :
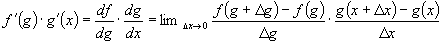
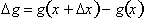
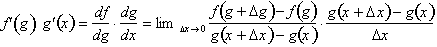
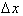goes to zero,
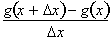
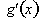or:
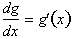
Similarly,
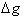also goes to zero as
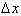goes to zero. Multiplying both sides by dx.
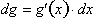
Thus as dx goes to zero;
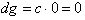
As dx goes to zero,
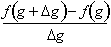becomes
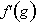. At the same time the
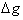in the denominator of
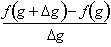cancels out with the
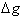in the numerator of
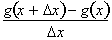, since they are both the equivalent. To conclude
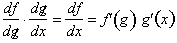
Thus the derivative of a function of
a function of x with respect to x,
is the derivative of the outer function with respect to the inner function,
multiplied by the derivative of the inner function with respect to x. Some
examples will show how this is done.
Next section ->
Section 6.1 - Motion, Velocity and Acceleration
