CHAPTER 9
Chapter 9 - The Derivative and its Approximations
In the previous section we studied
how we could generally approximate the graph of f(x) by studying only its first and second derivative. Now we will
develop further on the definition of the derivative to understand how we can
obtain accurate approximations of f(x)
using its first derivative only. Before continuing let me address a suspicion
that is growing in your mind. You are probably wondering why do we care about
using functions derivatives to determine the behavior of the original function?
If we want to analyze how f(x) behaves
we can go and graph it directly, without having to look at its derivative.
To answer this, recall that Calculus was defined as the study of
mathematically defined change. In science, changing situations are defined in
terms of several conditions or dimensions where one or more dimensions is
changing with respect to another dimensions.
We need Calculus to be able to define an instantaneous rate of change
for the situation. In such a case we need to work backwards from the derivative
that we defined to its anti-derivative.
The anti-derivative of the function will give us the exact relationship
between the situation and the changing dimensions. In order to understand how
to define an instantaneous rate of change and then calculate the net change,
the relationship between the function and its derivative must be fully grasped.
Therefore this chapter will take a look at the definition of the derivative to
see how it defines f(x).
Let us begin with the definition of
the derivative;
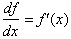
This gives us the exact change in
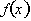 over the infinitely small interval dx. Remember how the instantaneous rate
of change was defined as taking the limit as a discrete value for a change in
x,
over the infinitely small interval dx. Remember how the instantaneous rate
of change was defined as taking the limit as a discrete value for a change in
x, 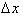 goes to zero.
goes to zero.

The derivative gives us the
instantaneous rate of change of a function over an infinitely small interval,
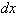 . If we multiply both sides by dx, we get:
. If we multiply both sides by dx, we get:
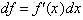
If we replace df and dx with
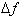 and
and 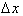 in the
above equation, then we get an equation that allows us to approximate the change in a function,
in the
above equation, then we get an equation that allows us to approximate the change in a function,
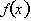
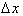 .
Since the derivative is only defined over an infinitely
small interval, we can not use its value to give us the exact change in a
function over an interval
.
Since the derivative is only defined over an infinitely
small interval, we can not use its value to give us the exact change in a
function over an interval
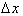 This is because the derivative of a function changes after
each interval, dx and is constant over the interval
This is because the derivative of a function changes after
each interval, dx and is constant over the interval
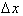 Therefore the following equation only represents an
approximation to the net change in
Therefore the following equation only represents an
approximation to the net change in
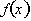 over a discrete interval
over a discrete interval
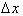 as it assumes that
the rate of change is constant.
as it assumes that
the rate of change is constant.
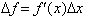
Look at the following graph and
notice how the approximation gets less and less accurate as
Δx
increases.
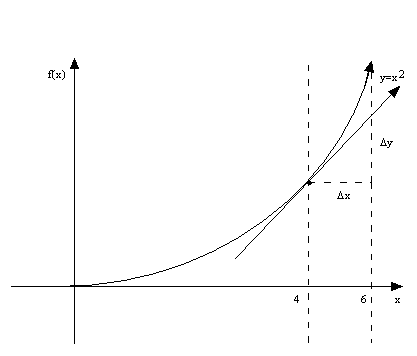
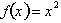 from x=4 to x=6,
from x=4 to x=6,
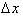 = 2. The change in f(x) over this
interval is by definition,
= 2. The change in f(x) over this
interval is by definition,
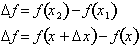
Substituting the
know values in:
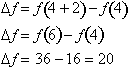
approximate this
change in
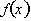 by evaluating the rate of change at x=4:
by evaluating the rate of change at x=4:
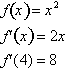
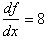 Replacing the infinitesimal values with discrete changes,
Replacing the infinitesimal values with discrete changes,
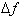 and
and
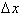 , and multiplying
both sides by
, and multiplying
both sides by
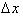 , yields:
, yields:
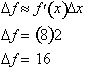
Using the
derivative we got an error of 4 or 20 %. As
Δx get smaller, the error gets less such that this method
becomes more accurate as
We can state our observations in a
short theorem:
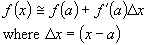
As long as we know a functions value
at some initial point
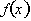 we can calculate its value at a nearby point x, by evaluating the derivative at x = a,
then multiplying it by
Δx=(x-a)
and adding the
Δf to f(a). This only gives an approximate answer because it assumes the
rate of change of the function is constant over the interval
Δx.
we can calculate its value at a nearby point x, by evaluating the derivative at x = a,
then multiplying it by
Δx=(x-a)
and adding the
Δf to f(a). This only gives an approximate answer because it assumes the
rate of change of the function is constant over the interval
Δx.
For example to approximate
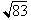 we can use
we can use
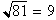 for f(a). The
derivative at this point is
for f(a). The
derivative at this point is

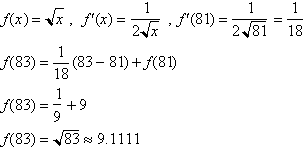
From the
calculator we get
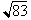 = 9.1104 which corresponds to an error of less than .01%.
= 9.1104 which corresponds to an error of less than .01%.
All that we have studied about the
derivative until now suggests that the entire graph of a function can be drawn
exactly by using the derivative only. This should be of no surprise since the
derivative of a function is derived from the function itself, it only remains
to undo what is done in the derivation to get the original f(x)
back, given only f'(x)
The accuracy of our results depends on how small our interval
Δx is.
This is because, with the exception of linear graphs, the derivative or rate of
change of a function is different at each and every point on
f(x).
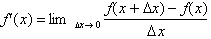
The change in the function is only
valid for the derivative evaluated at a point multiplied by an infinitely small
dx The derivative is only constant
over an infinitely small interval,
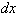 .
The only precise way of defining f(x) in terms of f'(x) is
by evaluating f'(x)
Δx
over infinitely small intervals, keeping in mind that f.(x) is different over each interval. Therefore if we multiply the
derivative by
Δx we get:
.
The only precise way of defining f(x) in terms of f'(x) is
by evaluating f'(x)
Δx
over infinitely small intervals, keeping in mind that f.(x) is different over each interval. Therefore if we multiply the
derivative by
Δx we get:
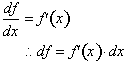
The change in f is exactly equal to the derivative
evaluated at a point x, multiplied by an infinitesimal dx. To get accurate approximations of f(x) we need to divide the interval into
smaller sub-intervals and evaluate the rate of change at each point. For
example if we were to divide the interval from x=4 to x=6 of
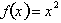 into 3 intervals to
calculate the change in the function.s value from x=4 to x=6 we would have:
into 3 intervals to
calculate the change in the function.s value from x=4 to x=6 we would have:
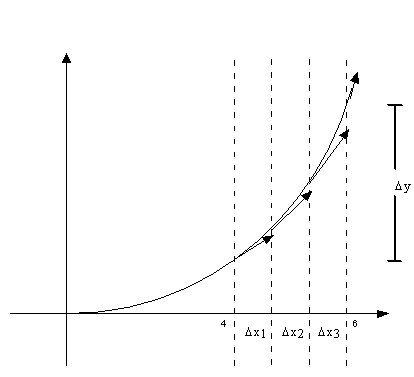
Direct calculations tell us that
from x=4 to x=6 , the change in f(x) is:
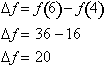
We
now want to find this answer using the derivative only. As opposed to our last
example we have divided the interval into three sub-intervals where the rate of
change is different at each of the three points. In each subinterval
Δx =
2/3 =0 .67.
From x=4 to
x=4.67 the approximate change in f
over this interval is:
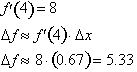
From x=4.67 to
x=5.33 the approximate change in f
over this interval is:
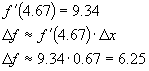
Similarly for
the last interval the approximate change in f
is:
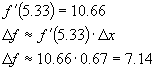
Therefore the net change in f(x)
over the interval from x=4 to x=6 is the sum
of the three approximate change in f.s that we calculated. Before stating the
results let me first explain some of the notation about to be used. The first
sign is:
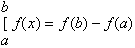
This
tells us to evaluate the change in a function,
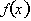 from two points
endpoints, x = a to x = b. The second sign is a summation sum:
from two points
endpoints, x = a to x = b. The second sign is a summation sum:
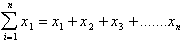
The summation signs tells us to add
up all the individual values of x from
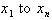 . Returning back to original example we can state our results
as, the change in the
. Returning back to original example we can state our results
as, the change in the
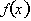 from x=4 to x=6 is
approximately equal to the sum of the
from x=4 to x=6 is
approximately equal to the sum of the
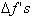 calculated for each
interval. Mathematically this becomes:
calculated for each
interval. Mathematically this becomes:
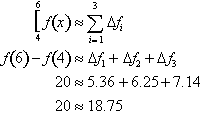
The summation
sign can also be written as:
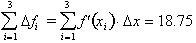
The result corresponds to an error
of just 6.6 %, far better than the 20% error we got when we used only one
interval of
Δx = 2. The reason we still
have an error is due to the fact that the derivative is constantly changing
over the discrete interval,
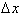
We only calculated the derivative at
three point from x=4 to x=6. The
accurate way to find the precise change in the function would be to let
Δx go
to zero and then calculate the infinite sum of the
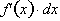 along the interval from x=4 to x=6. This is true because
according to the definition of the derivative, the rate of
change of a function at any point is based on
along the interval from x=4 to x=6. This is true because
according to the definition of the derivative, the rate of
change of a function at any point is based on
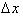 going to zero:
going to zero:
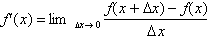
Thus the derivative is defined to be
constant only over an infinitely small interval, dx. We shall study this more in depth in the next chapter. Until now we can state the following
conclusion:
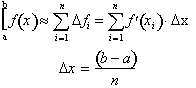
As n gets
larger,
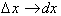 ~= 0
and our approximations become exact.
~= 0
and our approximations become exact.
Next section ->
Theory of Integration