CHAPTER 11
Chapter 11 - Understanding Integration
Section 11.3 - The Systematic Approach to Integration
Integration is a step-by-step
process used to analyze functions that are changing. While studying the
geometric applications, it was often easier to simply look at the graph and
identify a differential element that corresponds to a physical situation such
as an area or volume. Such a direct approach is generally not recommended since
most applications of integration are entirely independent of any geometry. Furthermore
the direct approach does not reflect any logical method or orderly analysis.
For these reasons we shall study a systematic approach to integration that is
applicable to any changing situation.
By letting x and f represent
something other than mere abstractions we will need to integrate our
mathematical functions in a more systematic and obvious method. As we shall
see, setting up integrals is often complicated by the presence of other dimensions
in the equations such that success is determined by realizing which are
constants and which are variables. The best way to get a proper grasp of what
is going on in the following series of examples is not to feel overwhelmed by
the apparent complexity of the situation.
We will first present a four step
procedure for setting up an integral and evaluating it. This is called the
systematic approach to integration and is derived from our understanding of
integration as summation process involving one changing dimension.
Step
1- Determine the form of the functional relationship between the
interacting conditions. This is synonymous with writing the equation, where
every dimension is assumed to be a constant:
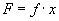
Step
2- Identify which dimension is changing with respect to another
dimension and determine the independent
variable. If f were given as a
function of x, then its value would
change as x changed. Thus x
is our independent variable.
Step
3- Write the differential dF,
as a product of f(x) and an infinitely small change in the independent variable
x, dx.
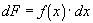
Step
4- Integrate both sides of the function from some value x=a to x=b to calculate the net change in the dependent dimension F.
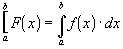
To understand how to apply the systematic approach, Consider
the problem of finding the work done by a gravitational field on a space
shuttle. Jules Verne, the master of
science fiction, wrote in his popular book Round the Moon about a space
shuttle that was launched into orbit by literally firing it from a large cannon
with a long muzzle. The ship veered of course and instead of landing on the
moon, it flew towards the side of the moon, around the dark-side or back of the
moon then came out the other side, directed towards earth. Luckily it did find
its way back to earth safely, by landing in the sea. Enough said of that, the
problem we want to consider is how much TNT would be needed to send the shuttle
to the moon.
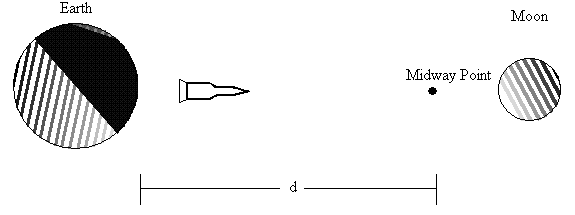
There are essentially two forces,
both due to gravity, acting on the shuttle. That of the earth, which attracts
the shuttle back towards the earth and that of the moon which attracts it
forward. The equation for the gravitational force between two bodies is given
by Newton's Law of gravitation is
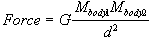where G is a
constant, M the mass, and d the distance between the two bodies. The derivation
of this formula is not difficult but what exactly is gravity and what causes
it, nobody knows. The fact is that there is an observed force determined by
this equation.
We can simplify this problem by
finding the location of the point where the gravitational force of the earth is
equal and opposite to the moons gravitational force. We do this by setting the
two equation equal to each other:
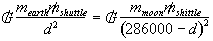
Solving for d
gives us 200,000 km from the center from the earth, remember gravitational
forces are measured from the centers of the body. Once the shuttle reaches this
point, the moons gravity will be stronger than the earths and will pull the
shuttle towards it. No extra energy will be required.
We can now state the problem as find
the total amount of energy required to send the shuttle to this midway point.
Then use this answer to determine how much TNT to use. In our systematic
approach. step one is to always
write the equation first. In this case we are looking for total energy and
energy is given by the simple equation:
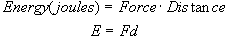
Step two is to
identify which variable is changing, or which
variable changes with respect to another constant. From the given
equation for gravitational force between two bodies we had force given as
function of distance:
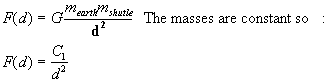
There are two
forces acting in opposite directions on the shuttle, that of the earth and that
of the moons, where the earth's force will always be greater till the midpoint
is reached.
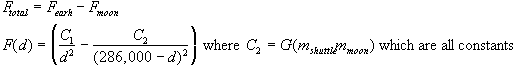
We can now write
the equation:
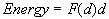
This tells us
that as the force is changing with respect to the distance and is not constant
over a distance d.
In step three we determine our independent variable and then write our
differential over an infinitely small interval. From the above equation it is
clear that Energy is entirely dependent on distance which tells us that d is
our independent variable, since everything else, including force, is dependent on it.
We can now turn the d after the f(d) into an infinitely small
Δd.
When doing this we must then convert the Energy also into an infinitely small
ΔE.
This tells us that the force at a particular distance, multiplied by small
distance
Δd
gives the energy done by the force over that interval or:
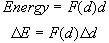
In the fourth and final step we determine which values, the dependent
variable goes from and ends at. These values become our limits of integration
so we can now take the infinite sum of F(d)
Δd over an interval to find the total energy done. In our
example the distance goes from the radius of the earth, 6400 km to the
midpoint, 200,000 km away:
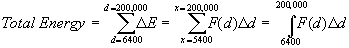
Replacing F(d)
with the value we derived it to be gives us:
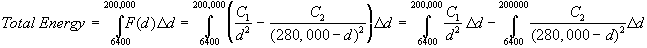
Evaluating this
integrals gives us:
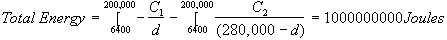
Therefore the
shuttle must have at least 100000000 Joules of energy before leaving the
earth's atmosphere, by the time it reaches the mid-way point it will have
almost no energy left as all was used up by the opposing gravitational pull of
the earth and the moon. Given that 1 kg of TNT will give 10 Joules of energy,
10000000 kg of TNT will be needed to blast the shuttle out of the canon.
