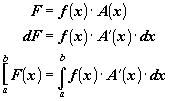Chapter 12 - Differentials

We have at last arrived at the final chapter of this book. The goal of this chapter is to extend the systematic approach of integration to include other types of mathematical functions involving relative change of variables. The process of identifying which dimension is changing with respect to another one is the first step in the systematic approach. The second step involves defining an instantaneous change for the function by writing what is called a differential. Differentials are of the form:

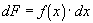
Dividing both sides by the infinitely small, dx, defines the derivative or instantaneous rate of change of 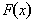with respect to x. What is important to understand is that 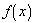is assumed to be constant over the interval, dx. Thus the infinite sum of these dx. s is given by integrating the function. The net change in the function, F(x) , over an interval form x = a to x = b is thus:

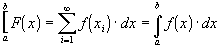
Let us now look at various combinations of f(x) and x, and see how we differentials are defined for each case. Consider case 1, where some situation, F is a function of two independent conditions f and x,

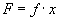
If f is a function of x, f(x), then its value changes as x changes. The differential is defined by converting the independent x into an infinitely small dx.

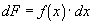
The differential is then integrated to determine how much the situation, F,  changes as x changes from x = a to x = b.

Consider case 2 where F is a function of two independent conditions, f and

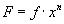
In this case, 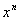represents a fixed or constant condition. We can replace A with 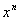to get:

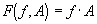
If f is given as a function of x, then we will first have to re-write f(x) as a function of A. We know that:

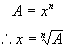
If 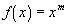, then 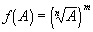. Once we have 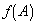, we can write our differential;

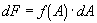
We can then integrate this function from some value of 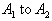. Keep in mind that,

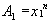
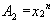
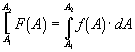
This approach to writing and integrating the differential for case 2 functions is confusing and abstract. An easier and more logical approach is to integrate with respect to x only: For example if,

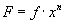
First let 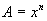, then 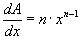or:

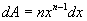
Substituting this back into the function yields:

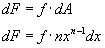
If f is a constant then from x =a to x = b, the change in F is:

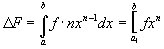
The result is the same function we started with. If f were a function of x, then its value would change as x goes from a to b. The differential can be written as:

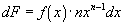
Integrating this function over an interval from x = a to x = b results in

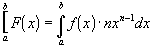
This results in the same numerical answer as the previously defined method of writing the differential.

To summarize, if 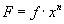; and f is a function of x, then:

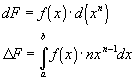
Here 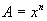, where

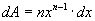
The third case of writing a differential is for functions of the form:

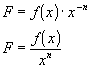
Once again, 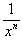is a constant factor that defines F. We can let 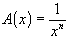, then:

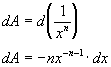
Substituting this back into case three:

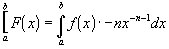
Our results can be generalized as follows. If F is a function of two variables, f and x such as:

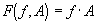
If A is some function of x, and f is also a function of x then both these values change as x changes. It is important to understand that is a constant value, dependent on x, that defines F. Therefore, the differential is defined as:

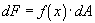
Since A is a function of x, then:

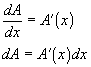
Substituting this back into the differential gives us the general expression:

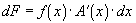
We can integrate this over any interval of to find the net change in F over the interval. Our results can be generalized for any combination of 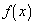and 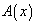, where 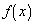and 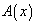can represent any function of x. The differential and integral is: