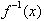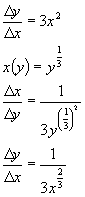Chapter 13 - Inverse Functions

In the second part of this book on Calculus, we shall be devoting our study to another type of function, the exponential function and its close relative the Sine function. Before we immerse ourselves in this complex and analytical study, we first need to understand something about inverse functions.

The Inverse function is by definition a function whose output becomes the input or the dependent variable becomes an independent variable. For example given the function:

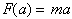
Which is Newton.s second law, or the force acting on a body of mass, m, is a function of the acceleration given to it. We are free to input any a and what we get out is the force. The inverse of this Force function, according to the definition, will give us the acceleration as a function of Force. This is done by simply solving for the independent variable, a:

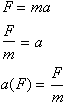
Now I can let F be anything and then find the acceleration as a function of it.

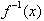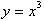The inverse of a function, f(x), is commonly written as, . Now we will look at the more general case of graphing a function and its inverse in the same co-ordinate planes. Given the function , to calculate its inverse we only have to solve this for x to get 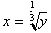. Notice that we have not really changed the function at all, we have only solved for the independent variable. The graph of these two functions would be exactly the same. Our definition of the inverse function therefore has to be slightly modified. After finding the inverse of a function we just interchange x and y to get:

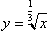
What does this do to the inverse function? This essential flips the graph of f(x) about the line y=x such that for every point (x,y) there is a corresponding point (y,x) on the graph of the inverse function. Now both the functions can be graphed in the same x-y plane.

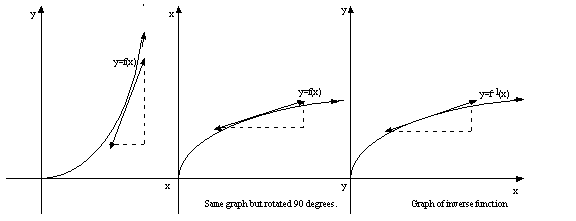
Remember that if we just solve for the dependent, we are not changing the equation but merely re-writing it. For this reason its graph is the same. By flipping the x and y, we get another function of x, whose relation to f(x) is that it has been graphed as though the x-axis were the y-axis and vice-versa. It is best we look at the two graphs:

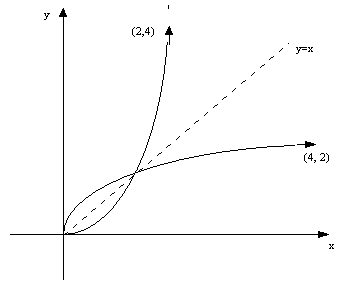
Notice how every point (x, y) has a corresponding point (y,x) on the inverse function. The graph of the inverse function is therefore exactly the same as the original function except that the x and y-axis have been switched:

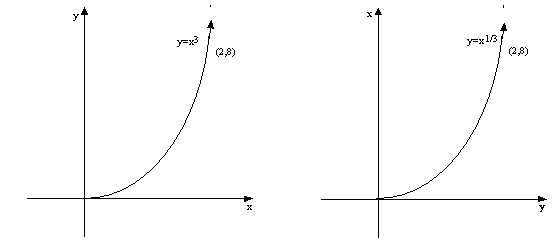
Since every point (x, y) has a corresponding point (y,x) then any point y from the inverse function when inputted in the original function should yield x:

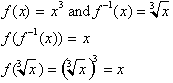
Remember the a function and its inverse are both function.s of x. The way they are related is that the inverse function represents the original function by just having its dependent and independent variable switched around. As you can see from the first graph, when the two function.s are graphed together, the inverse function contains all the point (x, y), of the first function, plotted as (y, x) with the exception that y is given as function of x. For this reason

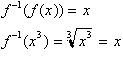
What is important to understand about the inverse function is that it is obtained by solving for the independent variable, then replacing it with y, to create a function that is also a function of x and can be graphed along with the original function.

Now that we know how a function and its inverse function are closely related, it brings us to the question, how are the derivatives related? Logic would tell us that instead of 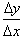we should just find 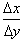by taking the reciprocal of the derivative. For example if we had:

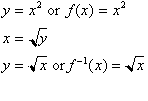
The derivative of the inverse function might be:

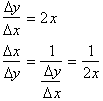
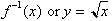
Or the derivative of is 1/2x. But this is not the case, the derivative is:

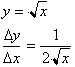
Let us examine the graph of f(x) and its inverse function to see what exactly is going on.

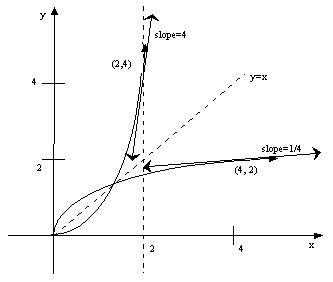
Note that at x=2, the slopes are not reciprocals but are reciprocals only at y values of on the inverse function or through (x, f(x)) and (f^-1(f(x)), x). Or the point (3,9) will have a reciprocal slope at (9,3) since at this point x and y are reversed hence the slope becomes the reciprocal or 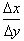This is the important point to understand about the function and its inverse, they only behave as opposites at point (a,b) and (b,a). This means that at point a something different is going on. The question is then how can we find the derivative of the inverse function with respect to the x-axis? Looking again at:

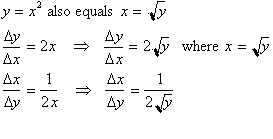
By replacing x with y and y with x in this last expression we get:

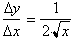
What we have just done is calculated the derivative of the inverse function only by looking at the original function and its derivative. The reason the derivative was not just the reciprocal of y=2x was because we forgot to do the following two steps:

1) Replace x with its equivalent expression in terms of y.

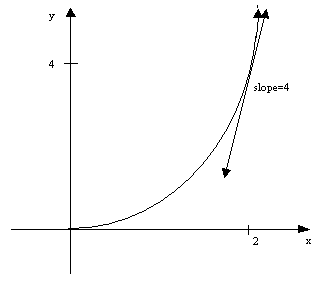
The slope in the following graph is 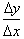at x=2 the slope is (2)(2)=4

By replacing x with we can find the derivative with respect to the same x-axis but instead with a y-value.

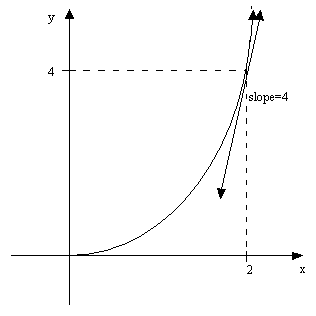
At y=4 the slope is 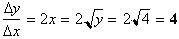which is the answer we got using x=2 instead.

Since the inverse function is graphed in the same xy plane as 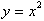, we can find the derivative of the inverse function with respect to the axis by taking the reciprocal of the expression 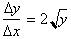and then replacing every y with x and vice-versa.

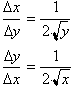
This last expression is the derivative for the function.s inverse with respect to the x-axis.

To summarize we can state the following theorem:

To find the derivative of the inverse function,

1) Remember, an inverse function is related to the main function in that if you reflect it over the line y=x, you will land on the main function.

2) First find the derivative of f(x)

3) Replace any x in the derivative with its y-equivalent, so as to be able to find the derivative with any given y-value.

4) Take the reciprocal of the derivative to get 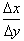so as to be able to find the derivative with respect to the y-axis.

5) Since the inverse function is graphed with respect to x, replace every y with x and x with y to find the derivative of the inverse function.

To summarize further:

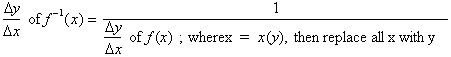
For example given 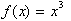find the derivative of its inverse,