Chapter 15 - Logarithmic and Exponential Functions

The previous chapter was devoted to defining a new type of function, the exponential function. The base of this function was multiplication. We can describe the exponential function as simply:

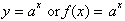
This is defined for all values of x, as defined in the previous chapter. Let us now look at the inverse of this function or what we shall refer to as the Logarithmic of this function. Remember the inverse function is found by interchanging y and x so we get:

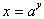
By solving for y to get the inverse function we get:

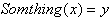
This tells us that we must do something to an inputted x value to find y. Remember x refers to the number we get by raising a to some power y. Therefore if we were given x then in order to get y, we must ask ourselves to what power has, a, been raised to so as to get y? This question can be replaced with the word . Log., where the Log, base a, of a number is the power a or the base has been raised to so as to get x. Stated mathematically:

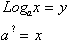
The question marks refers to our output or y values. Remember we are inputting values of x, making x our independent variable, then calculating what power the base must be raised to get x. This answer is our dependent variable as its value depends on what number x we have inputted. Hence:

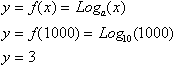
This is really not that difficult, just remember that the Logarithmic function is the inverse or opposite of the exponential function.

Now let us move on to examine some unique properties of the Logarithm.

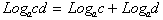
Or the Log of a product is simply the sum of the Log.s of each number. To understand this, recall the property of exponential multiplication, where the product of two exponential numbers of the same base is simply the sum of the exponents with the same base.

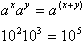
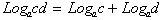we begin by assuming that c and d can be expressed as some exponent of the base. Remember that 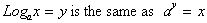. Therefore we can let:

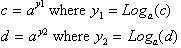
This means that 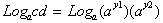by substituting c and d for 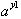and 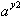respectively. Then:

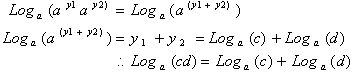
The second important property of Logarithms is that:

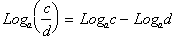
The proof is based on property 1, excepts that we must keep in mind that 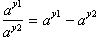. Thus 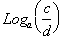is expressed as difference of two Logarithms and not a sum, since we are dividing not multiplying.

The final and most important property of Logarithms is that:

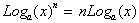
The proof of this extremely useful property requires us to first re-write 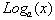as 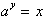where 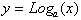. When we raise x to the n'th power we must raise the left side of the equation also to the n'th power:

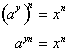
This is based on  the third property of exponential functions that tells us that an exponents raised to an exponent can be reduced to the product of the exponents. We can now write 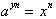as 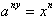which is the same as

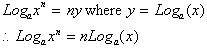
Having proved the unique propertied of Logarithms, all of which related to the property of exponents, we shall now calculate the derivative of the logarithmic function. We begin with the function:

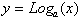
From the definition of the derivative:

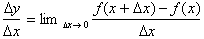
Using this we get:

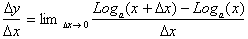
From the second property of Logarithms the numerator:

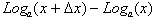
Can be simplified to:

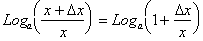
Substituting this back into the definition of the derivative we get:

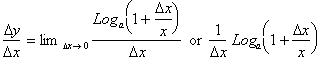
Recall the third property of Logarithms; 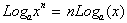Consequently:

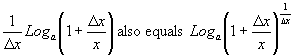
Clearly as 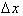goes to zero, 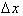/ x also goes to zero regardless of what value x is. Outside the brackets, 1/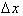 tends to infinity as 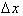goes to zero. This means we can rewrite:

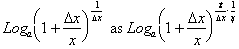
x / 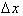is therefore the reciprocal of 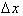/ x and it also tends to infinity as 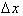approaches zero, regardless of what value x takes on. Thus from the third property of Logarithms:

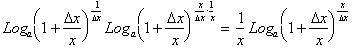
We shall now make a small change in variables to help evaluate the limit inside the Log brackets. We replace 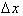/ x with 1/n and x / 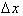with n. The derivative can now be re-written as:

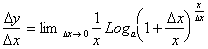
which now becomes

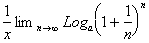
Let us now evaluate the limit an n -> infinity of 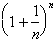. By the Binomial Theorem we get:

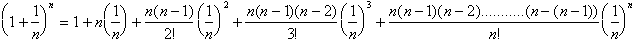
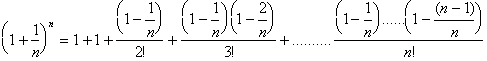
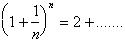
The sum of the terms after the first two will always be less than  the sum of the corresponding infinite series 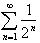whose sum can be proven to be one. Just think that it will take an infinite number of steps to cover one meter if in each step you can only cover half the remaining distance.

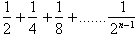
This is true because: 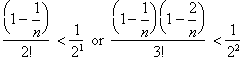. The same reasoning can be applied to the remaining n terms; the numerator will always be less than one and the denominator will be greater than the denominator of the corresponding n.th term in the series. For example:

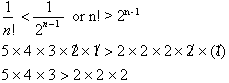
Since the sum of this series is 1, we can make an important conclusion,

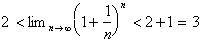
As we shall see later, this limit tends to the number e, where e=2.71828...Returning back to our derivative we get.

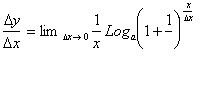
Therefore:

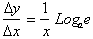
If the base a was set equal to e, we would have:

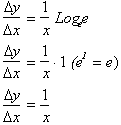
For this reason we denote the Logarithm of base, e, to be called the Natural Logarithm or ln x , whose derivative is simply 1/x .The derivative of logarithms of other bases is 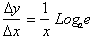, where the Log e is some other constant other than 1.

Having shown that the derivative of ln x is 1/x we can go on to prove the derivative of the inverse of the logarithm function, the exponential function, using our algorithm presented in the chapter on inverse functions. Before doing it that way let us use the definition of the derivative to find the exponential function.s derivative.

To do this we follow similar steps to those we used to calculate the derivative of the Logarithm of base a, function. Instead of

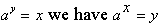
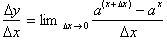
Recall the first property of exponential multiplication, where

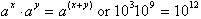
Therefore 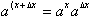and

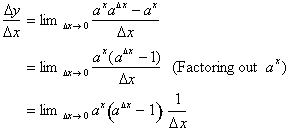
As 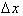gets closer and closer to zero,

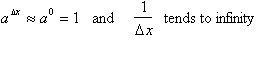
We will now make a small change in variable to simplify the limit calculation. We replace 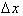with 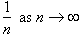. We now have:

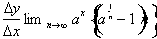
Let us now evaluate the limit in the brackets.

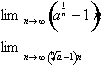
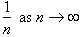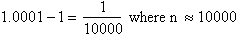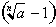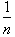
The value within the parenthesis will tend to zero or since for example . We now want to solve for 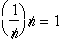and the derivative will be

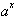
Solving the part in parenthesis gives us:

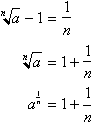
Raising both sides to the n.th power, we get:

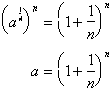
Remember we are taking the limit as n goes to infinity so we have:

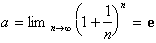
This tell us that if the base a were equal to e the derivative of

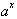
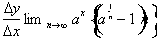
Becomes:

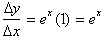
The reason  we get 1 is because:

Setting a equal to e gives us:

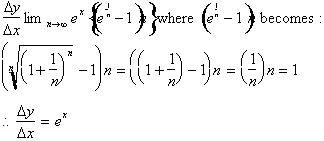
Remember this only happens when a=e. The derivative of 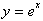is 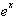or the function itself. This tells us that the rate of change of the function at a point x is proportional to the function.s value at that point. This will be discussed further in the next chapter.

Now let us examine the graphs of the Natural Logarithm function, 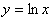, and the exponential function of base e, 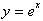. Remember these two functions are inverses of each other, since only the dependent and independent variable have switched places, or x and y.

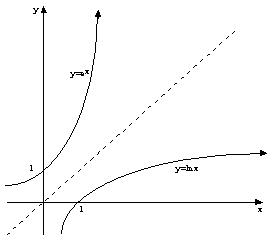
Since we know that the derivative of y = ln x is simply 1/x, we can then find the derivative of the inverse function, the exponential function, with respect to the x-axis,  using our algorithm presented in the chapter on inverse functions. It goes as follows:

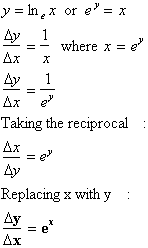
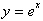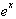We have just found proven that the derivative of is the function itself or y. = y. This was done by just examining the function.s inverse, the natural logarithm and its derivative with respect to x. This shows the close relationship the Exponential Function has with the Logarithmic function, the two being inverses of one another. This concludes our study of these two function.s and their derivatives. We will explain later how e is actually a number defined as a limit. For now just consider how in calculating the derivative of the multiplicative function, the exponential function, involved an analysis of each term in the series of the binomial expansion, whereas in the study of repetitive addition functions, polynomials, all the terms except the second, went to zero.