CHAPTER 19
Chapter 19 - Differentiating and Integrating the Sine function
In the previous chapter we underwent a long and thorough analysis of just defining the Sine function mathematically. This was done with by calculating the arc length of a circle, the inverse sine of x being the arc length from zero to x. The goal of this chapter is to differentiate and integrate this function and as we shall soon see, the sine function will be unlike any other function studied so far.
From the definition of the inverse sine or arcsine function we have:
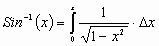
Once again if you recall from the Chapter on inverse we learned that
a function and its inverse are essentially the same function. We can
therefore easily find an expression for 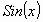 based
on the definition for
based
on the definition for 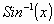 . The only problem here is
that we have to integrate
. The only problem here is
that we have to integrate 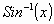 before we can find a
way of expressing
before we can find a
way of expressing 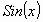 . We do however know how to
calculate the derivative of
. We do however know how to
calculate the derivative of 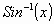 . From the
definition of the integral it is:
. From the
definition of the integral it is:
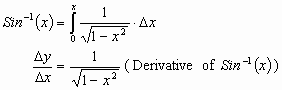
By following the algorithm presented in the chapter on inverses for finding the derivative of a function’s inverse we can find the derivative of the Sine function without having found a way to define it yet.
We first replace any x with its y equivalent so as to be able to find the derivative with any given y-value.
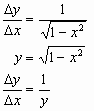
From the graph of the circle this tells us that the derivative of the inverse sine
function is just 1 over the y value of that particular arc length.
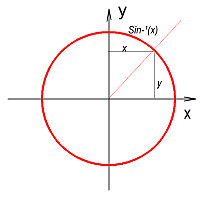
From the graph you can see that this value corresponds to the Cosine of the arc length or angle by the definition of the Cosine Function. Therefore:
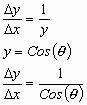
There is one important difference to keep in mind. The  in the left side refers to the derivative of the inverse Sine function or arc length function of x. Therefore
in the left side refers to the derivative of the inverse Sine function or arc length function of x. Therefore  means a small change in the arc length. On the other hand the y in the
means a small change in the arc length. On the other hand the y in the 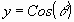 is just referring to the point until which this arc length is being measured in terms of the unit circle. We can now write:
is just referring to the point until which this arc length is being measured in terms of the unit circle. We can now write:
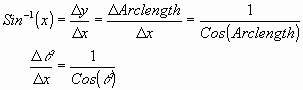
Remember arc length and 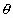 are the same thing from our definition of the angle. In the graph of the inverse sine function, x is our independent variable and
are the same thing from our definition of the angle. In the graph of the inverse sine function, x is our independent variable and 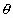 or arc length is our dependent variable. Since the Sine function is the inverse of the inverse Sine function, then
or arc length is our dependent variable. Since the Sine function is the inverse of the inverse Sine function, then 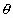 is our independent variable and x is our dependent variable. This means that the derivative of the Sine function is given by:
is our independent variable and x is our dependent variable. This means that the derivative of the Sine function is given by:

Since we already calculated the derivative of the inverse Sine function to be 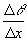 which is simply 1 over the Cosine of the angle, then the derivative of the Sine function is just the reciprocal of that:
which is simply 1 over the Cosine of the angle, then the derivative of the Sine function is just the reciprocal of that:
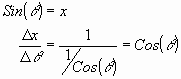
This important conclusion tells us that the derivative of the Sine function is just the Cosine of that particular angle or arc length. The Sine function inputs arc lengths and outputs the corresponding x-value of that arc length. Therefore its derivative with respect to arc length is just the Cosine of that arc length.
To find the derivative of the Cosine function first recall that 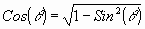
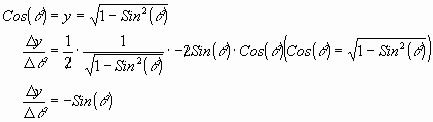 .
.
This tells is that the derivative of the Cosine function with respect to arc length is just the negative Sine of that arc length. To summarize:
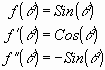
We have now found the derivative of the Sine function in terms of the Sine and Cosine of the arc length,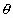 . There still remains the stumbling block, what is
. There still remains the stumbling block, what is 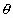 or arc length? Though we have shown rather crudely what is the derivative of the Sine and Cosine function are , we still have not found a way of defining
or arc length? Though we have shown rather crudely what is the derivative of the Sine and Cosine function are , we still have not found a way of defining 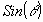 . The only obstacle was our definition for the inverse function:
. The only obstacle was our definition for the inverse function:
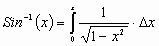
There is absolutely no way we can evaluate this integral. You can understand this in two ways. First the derivative approaches infinity as x goes to 1 and second from the graph of the circle, arc length is continuous never ending length. It goes round and round the circle forever. Though we have defined a beginning there is no end. It is this complex nature of the arc length of a circle that tells us that there is no way to solve its using real numbers.
It is what we call an irrational integral and can only be solved with complex or imaginary numbers, 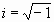 . The best way of thinking of what imaginary numbers are is that they are numbers that basically tell us there is no solution to the equation. There is nothing magical or transcending about them. If we ever see them, they only alert is that the equation has no solutions.
. The best way of thinking of what imaginary numbers are is that they are numbers that basically tell us there is no solution to the equation. There is nothing magical or transcending about them. If we ever see them, they only alert is that the equation has no solutions.
Using complex numbers the integration goes as follows:
First factor out -1 in the denominator:
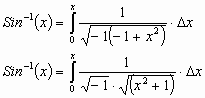
Factoring out a 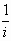 gives us:
gives us:
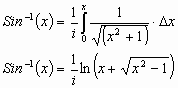
The derivative of 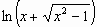 is:
is:
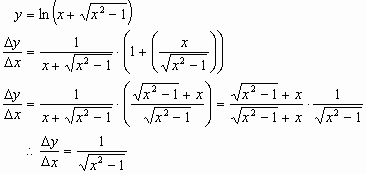
We have shown how 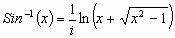 . Now
let us find an expression for
. Now
let us find an expression for 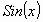 .
Since
.
Since 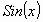 is
the inverse of
is
the inverse of 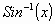 , we only need to interchange y
and x to solve for y, where y = arc length:
, we only need to interchange y
and x to solve for y, where y = arc length:
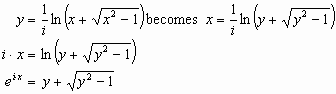
Factoring out a i or 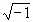 from
from 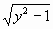 gives us:
gives us:
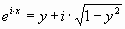
where 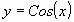 and
and  . This now reduces to the famous Euler’s equation:
. This now reduces to the famous Euler’s equation:
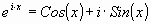
You might object to our replacing y with 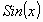 . Do
not forget that when
. Do
not forget that when 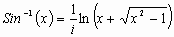 , y referred to arc length
or
, y referred to arc length
or 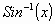 and
i interchanging x with y, y then refers to
and
i interchanging x with y, y then refers to 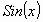 since
that is what we were initially calculating.
since
that is what we were initially calculating.
Euler’s equation probably makes little sense to you. All it really is is another way of expressing the relationship between the complex logarithm and circular functions ( Stillwell 221 ). The sine and cosine functions are therefore solutions to such irrational integrals.
There is still one way of defining 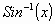 which is through an infinite series of terms based on the binomial expansion theorem, which defines an infinite series for sums raised to negative and fractional exponents:
which is through an infinite series of terms based on the binomial expansion theorem, which defines an infinite series for sums raised to negative and fractional exponents:
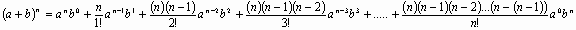
or more simply:
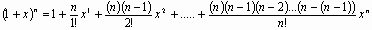
Though we will study infinite series in more detail in the following chapter, it would do no harm to begin the study with our inverse Sine dilemma.
As the expansion for 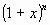 is valid for all values of n, then we are able to write the integral for
is valid for all values of n, then we are able to write the integral for 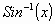 in a different way:
in a different way:
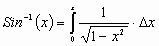
Which now becomes:
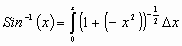
The binomial expansion is:
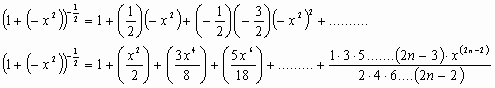
This is clearly an infinite series with never ending terms since 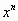 will
never equal
will
never equal 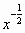 .
Integrating the series will give us the series for
.
Integrating the series will give us the series for 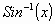
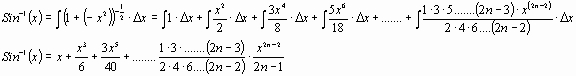
The series is valid for -1 < x < 1. For 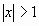 each term in the series will get larger, causing the series to diverge. We will talk more about how this series works in the next chapter.
each term in the series will get larger, causing the series to diverge. We will talk more about how this series works in the next chapter.
Summary
In these three lengthy chapters we undertook an in depth study of defining the Sine function. Beginning with the simplest definitions we moved on to defining its inverse function as an arc length:
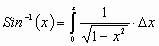
The 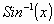 is in reality the arc length of a circle as a function of x or:
is in reality the arc length of a circle as a function of x or:

We showed how angles can only be measured in radians, a relative measurement that relates arc length to the rotation of two lines and the angle they define. Thus:
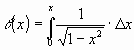
This relates degrees, measured in radians, as a function of x.
The integral being “un-integrable” due to the unique properties of the circle, could only be solved with imaginary numbers. We then went on to prove the complex relationship between the exponential function and the Sine function, or 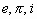 .
.
Last but not least we were shown, rather simply, how the inverse sine function can be expressed as an infinite series of terms based on the binomial theorem for negative fractional exponents. Our study of the Sine function will resume in the next chapter when we study the function in yet another way, actually the same way but by using some new theorems from Calculus.