Chapter 21 - The Mean Value Theorem

The Mean Value Theorem is a rather simple and obvious theorem yet the same can not be said about its implications in Calculus. Its proof will offer an important review of the definition of the derivative and the integral. Let us begin with the graph of 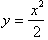and its derivative

Before continuing it is important to keep in mind that from the definition of the derivative, the derivative of 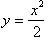, 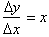gives us the slope at any point on the graph of

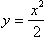
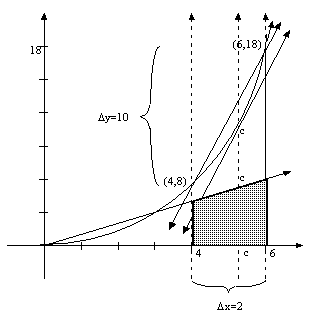
The area under the graph of the derivative from x=4 to x=6 is given by:

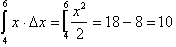
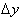, of the graph of the anti-derivative from x=4 to x=6 is exactly the area under its derivative bounded by the same interval. Remember from the definition of the integral:

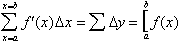
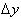we calculated to be 10. If we draw a line through (4,8) and (6,18), and draw an imaginary base of length 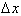, then we get somewhat of a triangle. The slope of this line is 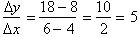. Therefore the area under the graph also equals the slope of this line multiplied by the change in x, 2 or 5*2=10.

Now we know that there is a point on 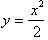the graph of between x=4 and x=6 that has the same slope as the line connecting the endpoints of the interval (4,8), (6,18). The reason we know that this is true is because the line connecting the two endpoints is the direct way to link the two points. Since the graph of 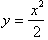takes a curved way to connect the points then somewhere along its path its direction must be parallel to the connecting line if it is to ever reach the endpoint.

Now that we know such a point exists and that the derivative of the graph is defined at every point, then the change in y, 10, can be found by finding the slope of the line that is parallel to the line through (4,8) and (6,18). This slope i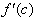s . This tells us that there exists a value c between 4 and 6, such that the derivative evaluated at this point c,  gives the slope of the line parallel to the line connecting the two endpoints on the anti-derivative. Since this line must lie between x=4 and  x=6, then c must also lie in this interval, and equals the value at which this line exists.

We can express this as:

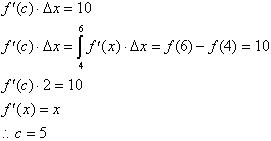
Our results can be generalized:

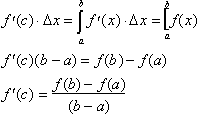
This is the mean value theorem; there exists a number c between a and b on the graph of f.(x) such that f.(c) gives the slope of a tangent through f(c) that is parallel to the line through (a, f(a)) and (b, f(b)). Conceptually speaking it is important to remember this as:

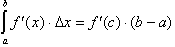
The area under the curve of a graph can be expressed either by evaluating the integral at the endpoints or by finding a number c, between a and b, and multiplying it by the change in x, (b-a). In other words the net change in a function.s anti-derivative can be found by just using the function itself. As we shall see, finding that constant, c, is another problem itself.