CHAPTER 24
Chapter 24 - Techniques of Integration
We have studied a
great variety of functions and their derivatives. Until now the process of
differentiation has been straight-forward and mechanical. For example
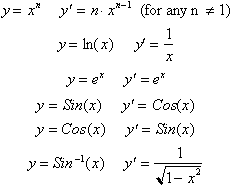
If in any of the above functions, x
was replaced by u, where u is another function of x, then by the Chain rule:
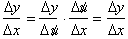
From the product rule, the
derivative of any product uv, the derivative was:
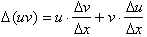
The
rules for Integration, as we already know are unfortunately not so
straightforward as in differentiation.
The reason for this is because there are numerous ways to write a
function, yet only one of these ways will resemble a differentiable form.
Therefore the key to integration lies in finding that integratable form and as
we shall soon see, that form is not necessarily the simplest form.
Let
us take a look at two simple functions and show the variety of ways it can be
simplified, expanded and re-written.
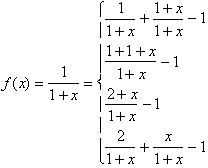
or another example:
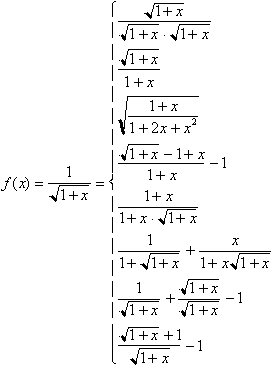
A reader pointed out an error in this last example. Two of the functions on the right are not equal to the left
one ( fourth and sixth one from the top ).
Even though all these functions are equal to the original function, they can not be
integrated directly as they do not appear in a differentiable form. The only
two functions that can be integrated directly are the original functions
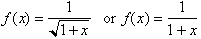 , whose integrals are
, whose integrals are
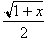 and
and
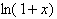 respectively. If you
closely examine the physically different, yet mathematically equal functions,
you can notice that in most cases the integrable form is quite evident and can easily be found with a few quick
simplifications such as:
respectively. If you
closely examine the physically different, yet mathematically equal functions,
you can notice that in most cases the integrable form is quite evident and can easily be found with a few quick
simplifications such as:
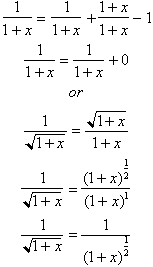
In other cases the distinction is
not so evident.
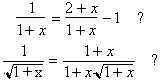
This final and important chapter is
devoted to the study of functions that at first glance look impossible to
integrate; however, after the application of certain simplifications and
re-writing techniques, the function can be integrated.
The
first of these techniques is called integration by parts. It allows us to
evaluate the integral of a product, in terms of the integral of one factor
multiplied by the derivative of the other. From the product rule we have.
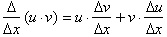
or just:
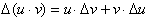
Integrating both sides gives us:
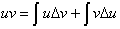
Solving for
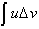 gives us:
gives us:
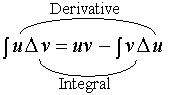
For example to integrate the
product of
Now that we have expressed the
derivative as a sum of
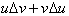 , we can integrate the derivatives to get:
, we can integrate the derivatives to get:
The
reason why this integration technique works is based on the product rule which
allows us to differentiate a product as a sum of two functions,
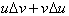 . Even when not integrating a product, one can always let
. Even when not integrating a product, one can always let
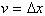 such that v=x.
such that v=x.
The
next technique that we shall study is based on the derivatives for the Sine and
inverse Sine function. From the previous chapter we saw how
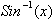 was defined as:
was defined as:
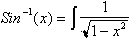
or by the definition of the
integral the derivative of
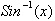 is
is
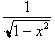 . Based on this the derivative of Sin(x) was found to be Cos(x).
. Based on this the derivative of Sin(x) was found to be Cos(x).
Furthermore
we showed how all other trigonometric function such as Tan(x) and Sec(x) could be
expressed in terms of Sin(x) and Cos(x), or just Sin(x) since Cos(x) is also
dependent on Sin(x). With this in mind let us see how we can express the
inverse tangent ans secant functions in terms of the inverse sine function.
The
function
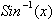 is defined as the
arclength from 0 to x on a circle or:
is defined as the
arclength from 0 to x on a circle or:
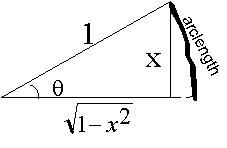
If
we define the inverse tan function to give us the ratio of the x value to the
y value for a particular arclength then:
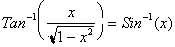
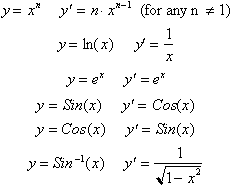
Where
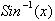 gives us an arclength
for that particular value of x, and the tangent of that arclength gives us
gives us an arclength
for that particular value of x, and the tangent of that arclength gives us
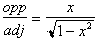 . If we let
. If we let
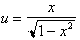 and then differentiate both sides we get:
and then differentiate both sides we get:
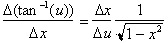
We
have found the derivative of
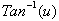 but we need to find
the derivative of
but we need to find
the derivative of
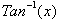 not
not
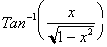 . To do so we first need to define
. To do so we first need to define
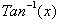 in terms of
in terms of
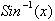 . The function
. The function
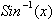 tell us the x value
for a given arc length. Now if for the same arclength , the Tangent were x,
then what would be the Sine of the Arclength. To answer this, let us consider
the following graph again: Error: The equations for square root of 1 - x^2 should all be 1 + x^2 in the
next few lines.
tell us the x value
for a given arc length. Now if for the same arclength , the Tangent were x,
then what would be the Sine of the Arclength. To answer this, let us consider
the following graph again: Error: The equations for square root of 1 - x^2 should all be 1 + x^2 in the
next few lines.
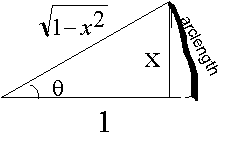
In
this circle, the tangent of the angle is x, and the Sine of the angle is
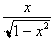 . Hence:
. Hence:
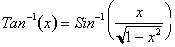
For any angle whose Tangent is x,
its sine will be
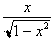 . Differentiating both sides yields:
. Differentiating both sides yields:
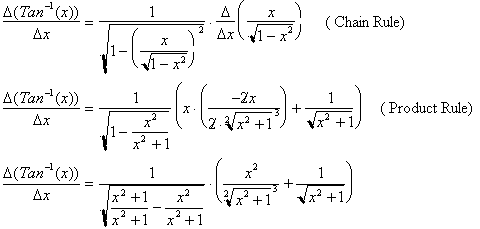
Further simplification yields:
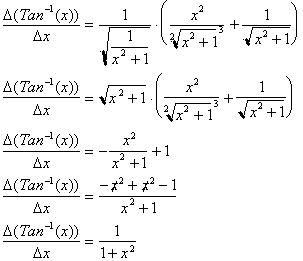
The derivative of the inverse
Tangent function is just
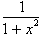 or more importantly.
or more importantly.
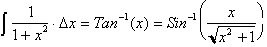
By similar means we can find the
derivative of other inverse trigonometric functions, by first defining it in terms of
the Sine of the angle and then differentiating it.
The
underlying concept in these definitions is the fact that the inverse tangent,
secant and any other trigonemetric functions can be expressed in terms of
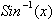 such that integrating
them is much easier as we already have them defined.
such that integrating
them is much easier as we already have them defined.
As
we mentioned before, the difficulty of integration lies in the fact that a
function could be written in so many different ways.