CHAPTER 5
Chapter 5 - Differentiating Functions
Section 5.2 - Differentiating Sums of Functions
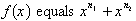which is a sum of two functions of x,
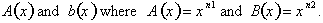Therefore, if
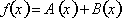What would
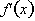be? The answer is
that the derivative is the sum of the derivatives of the two functions To prove
this let us return to the definition of the derivative.
We can express a small change in f,
, equal to
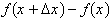. Therefore:
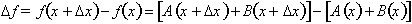
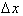and taking the limit
as
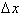goes to zero gives us
the instantaneous rate of change of f
with respect to x.
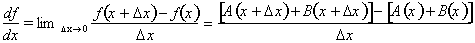
Combing the A(x) and B(x) terms together simplifies the above expression to:
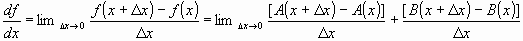
Which reduces to:
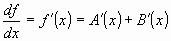
Therefore if f(x) is a sum of two
functions of x, then its derivative with respect to x is the sum of the derivatives of the functions
with respect to x. Thus:
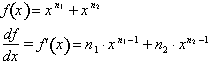
Similarly if f(x) is defined in
terms of a difference among some
functions of x, then
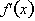is the sum of the difference among the derivatives of the functions.
Next section ->
Section 5.3 - Differentiating Products of Functions
