Chapter 20 - Applications of the Sine Function - Oscillatory Motion

Having gone through a long and detailed study of the Sine function the time arrives for us to study its applications. There are many applications of the Sine function, however, the most common are relate the dynamics of vibrating or oscillating systems. By oscillating system we mean any object whose motion can be characterized as a continuous back and forth never ending motion. Such motion occurs when the resistance to motion of a body in motion is directly proportional to the distance covered and acts in a direction that is opposite to the direction of movement.

The typical and simplest example of this is just a simple spring with a body or block of mass m attached to it.

If we assume that the block with mass m rests on a friction less surface then the block is free to oscillate with any horizontal force. According to Hooke's law the force required to stretch a spring is directly proportional to the length of the spring. Each spring therefore has a constant, known as the spring constant k which tells us the force required to stretch the spring a given distance.

For example if the spring constant, k, of a rather stiff spring such as those used in cars as opposed to a slinky, were 1800 newtons per meter or k= 1800 N/m then to stretch the spring one meter would require a force of 1800 Newtons and to further stretch it three meters would require a force three times as great or 5400 N. This is all in accord with Hooke’s Law, which states that the more you stretch it the greater the force required.

Consider now the block above of mass m at equilibrium position. By equilibrium position we mean the object is at rest with no unbalanced force acting on it. This tells us that the spring is being neither compressed nor stretched but is just lying there attached to the block. If we stretch the block a distance x from its equilibrium position and let go of it, then it will oscillate back and forth. Our goal is to mathematically describe this motion.

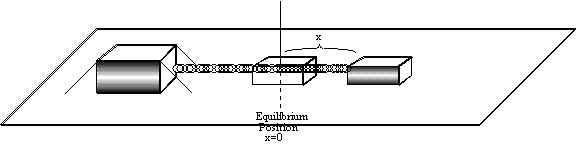
The amplitude of oscillation is 2x and the maximum force exerted by the spring on the block is kx. Keep in mind however that the force is zero at the equilibrium position , since the spring is un-stretched there and at this point the blocks entire energy is kinetic while at the endpoints of its oscillation it possesses entirely potential energy stored in the spring and its velocity is zero.

Since the spring exerts a force kx when stretched, the work done stretch a spring a distance x is given by:

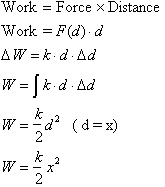
The work required to stretch a spring a distance x is equal to 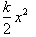. When any mass m is stretched a distance x then let go of it will be pulled back with a force that varies with the distance stretched.

The total energy of the system varies between kinetic and potential energy depending on the mass’s position. The kinetic energy of the block in motion is always equal to 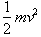, where v is its velocity at a particular point. At that point x the potential energy will be 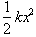or the energy used to stretch the spring to that position. The sum of the potential and kinetic energy of the block at any point is a constant that never changes. It corresponds to the net energy of the oscillating system:

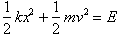
At x=0, the velocity is a maximum and when v=0, x is a maximum and the block is at its endpoint.

. Let us first solve the equation for v:

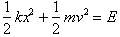
Multiplying both sides by 2 gives:

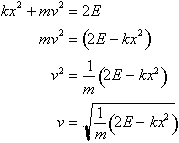
Now substituting velocity for 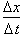and separating variable yields:

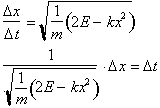
Integrating both sides:

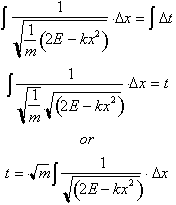
Recall that E stood for the total energy of the system. At its endpoints the velocity of the block is zero. The total energy is then equal to 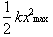where 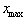equals half the amplitude of oscillation.

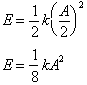
Substituting back into our integral gives us:

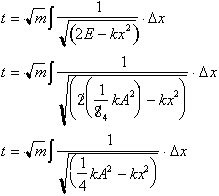
We can factor out a 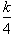from the denominator to get:

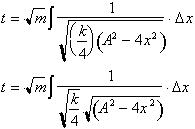
We can take out the constant 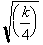from the integral to get:

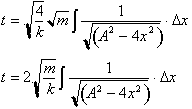
We can now factor out 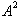from 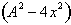and then remove the constant A from the integral to get:

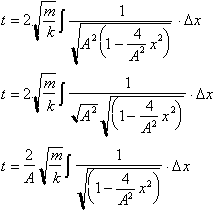
This integral now has the familiar solution that we have studied:

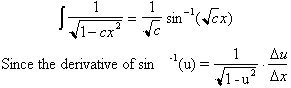
where 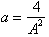and

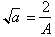
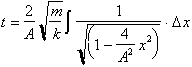
has the solution:

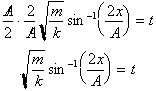
Now that we have solved it, how do we interpret it or make sense of this solution? Basically this solution tells us that the time required for the mass to a distance x from the equilibrium position. We can therefore easily calculate the period of the oscillation, the time required for the mass to complete one cycle. The period would be four times the time required for the mass to move from x=0 to x= 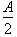. Substituting this into our solution gives:           

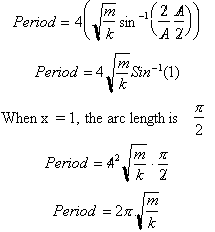
This answer tells us that the period of an oscillating mass on a spring is independent of the amplitude of the oscillation. For this reason springs are used in watches. Despite air-resistance and friction between the spring and other parts that would cause the Amplitude to gradually decrease over time, the period of vibration would remain unchanged.

Just as we are able to find time as a function of x, we can find x as a function of time using the Sine function or the inverse Sine Function. We saw that:

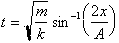
Multiplying both sides by 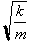gives us:

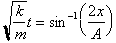
Taking the Sine of both sides just switching around the dependent and independent variable:

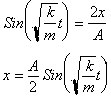
( Many physics books replace 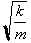with w, where w=2p f and f, frequency= 1/t, t= period = 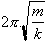. The reason being w stands for radians/sec and hence keeps the units in order and simplifies calculations.)

Now that we have the position x as a function of time we can differentiate the function one to find the velocity and twice to find the acceleration.

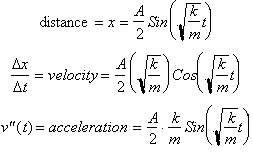
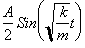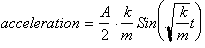This expression in with its original reference, x or position since 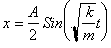. This now gives us:

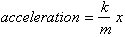
Since Force is by definition mass* acceleration, if we multiply the function for acceleration by m we get:

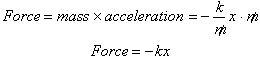
This is what we originally started with, Hooke’s Law. The force in a spring is proportional to the distance it is stretched and acts in the opposite direction of the motion to oppose the motion.

Before ending you might be wondering what happened to the constants? I decided not to put them in as to avoid any unnecessary variables or numbers that would impede your understanding of the important concepts being studied. The solutions with the constants included should here forth read:

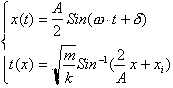
Summary

In this chapter we saw how in a spring the force required to stretch the spring is directly proportional to the length stretched. Recalling that  force is defined as mass* acceleration or F= ma, where acceleration is the second derivative of the position function of an object in motion:

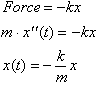
This can be rewritten as

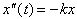
The only function whose second derivative is proportional to negative of the original function is the Sine function, since:

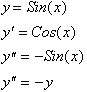
Therefore this chapter was in essence devoted to the understanding of how the Sine function and its derivative apply to applications where the second derivative is directly proportional to the negative of the original function. This is why the Sine function is restricted to Oscillatory motion, since a force -kx, will always act so as to oppose the motion of the body in any direction. From the Conservation of Energy the body will then rebound back in the opposite direction once whatever force acting on it brings its velocity to zero because all the energy will now have been transferred from the mass to the system. In such a way this back and forth process goes on forever until interrupted by other forces such as friction.