Chapter 14 - Introduction to Exponents

This chapter on exponents marks the beginning of the second half of our study of Calculus. In the first half we introduced the concepts of numbers, functions and graphs, then went on to analyze them in more depth using the derivative. Having understood what the derivative was, the remainder of the first half was devoted to integration, or the reverse of differentiation. It required some abstract thinking since what we were doing was analyzing that which we could net directly see.

The first half we basically focused entirely on simple rules of arithmetic. Differentiation was presented as a subtracting and dividing process while Integration was shown to be a multiplicative and additive operation. In other words our study of Calculus was limited to multiplication and addition. From the first chapter you might recall how multiplication was defined as  repetitive addition where x multiplied by y was just x plus itself y times. With this idea we can say that all multiplication reduces to addition and this means our study of Calculus was based entirely on addition.

Now we will study Calculus based on multiplication through the study of exponential and Logarithmic function. Before continuing we need to establish a few properties of exponents. The rules that govern exponents are very similar to addition. The definition of an exponent or a power is:

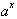
Where a is called the base, and x is the exponent or power. Therefore a raised to the x power is defined to be:

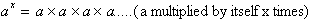
For example:

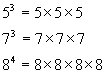
Compare this with the definition of multiplication where:

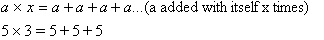
Since multiplication can be called repetitive addition then exponent or raising something to a power can be though of as repetitive multiplication. This is really all that we mean by exponents. They can be reduced to multiplication and multiplication can be further reduced to exponents.

Now let us take a look at some properties of exponents. The first being the rule for multiplying two exponents of the same base.      

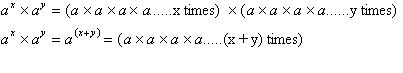
Notice how multiplication of exponents has been reduced to addition of exponents. For example:

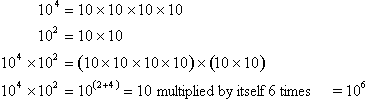
It is really this simple. The second important property of exponents states that a to the x power raised to the y power is just a to the product of x and y power or:

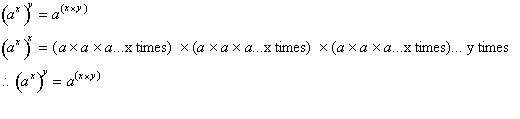All this is saying is that an exponent raised to another exponent can be reduced to multiplying the two exponents out or:

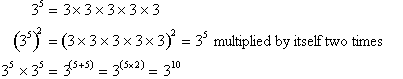
Take note of how this rule reduces exponents of exponents to just multiplication of the two exponents whereas rule one reduces multiplication of exponents to addition of exponents, ( assuming a common base a).

These two important properties of exponents are the fundamental ways of defining what exponents are and how they relate to repetitive multiplication, where multiplication is just repetitive addition. It now remains for us to define what we mean by raising an exponent to a fractional power. This is actually much simpler than it sounds.

Since we defined whole number exponents to denote repetitive multiplication, we would want fractional powers to represent repetitive division. Fractional exponents therefore are called roots and tell us into how many equal multiples a number has been divided into ,such that the product of these roots gives us the original number a back.

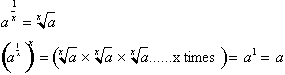
This definition of fractional exponents remains consistent with the first and second rule of adding and multiplying exponents.

Last but not least we need to define what we mean by raising exponents to negative numbers. This is done by remembering that positive exponents  refer to multiplication, therefore negative exponents would refer to division. In order for our definition to remain in accordance with the two rules of exponents we need to define it this way:

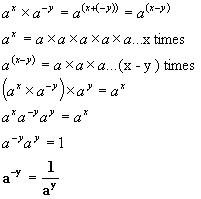
This is rather a long way of deriving this as you can clearly see from the following example how negative exponents are defined.

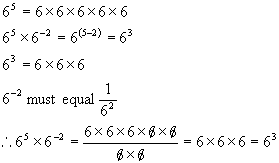
Increasing the power means multiplying it more times by itself, while decreasing the power means dividing it more times by itself. Therefore multiplication and division reduce to addition and subtraction in exponents.

Since a raised to the first power is a multiplied by itself once, or just a, by definition then what is a raised to the zero power. Once again this definition must remain consistent with the rules of exponents. Instead of raising a to zero power, we can raise it to 1/∞ or one over infinity which is close to zero. Therefore a raised to the negative 1 over infinity is:

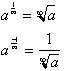
From the definition of fractional exponents,  we are asking ourselves what number multiplied by itself an infinite amount of times gives a? If this number were slightly less than 1, then as you multiply infinite times, you get a smaller and smaller number or zero. If this number were slightly greater than 1 then you would get a larger and larger number each time you multiply it by itself, or eventually infinity. Therefore only the number one satisfies both limits as you approach it from either 1/∞ or -1/∞. Hence:

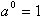
You might think that how can: 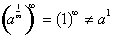. This is because zero and 1/∞ are not exactly the same.

This definition of zero exponent power tells us an important property of exponential.s. In multiplication you are adding, where adding nothing is zero. In exponents you are multiplying, where multiplying nothing is one, not zero. Therefore all exponents are expressed as repetitive multiplication of numbers greater than or equal to one. We can say that the base of exponents is therefore 1.