Chapter 18 - The Sine Function- Definition

Until now we have restricted our study of the Sine function to triangles where:

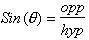
Remember a function is by definition only a function when the output is directly related to the input. For example the following function gives the Volume of water in a bowl as function of height:

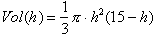
Input any height and one can easily calculate the volume. However the function,

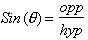
is not a function as none of the variables; opposite, hypotenuse, or angle (theta) are related in any way. Give me an angle and I can not give you the Sine of it, that is without looking it up in some table.

To begin our study of the Sine function, we need to first find a way of defining it as a mathematical function, such that the Sine of an angle is a function of the angle inputted. It therefore behooves us to define what exactly is an angle. Till now we have assumed an understanding of angles and we looked at Triangles to show what they mean. Before defining what an angle is, let us now take an important look at circles to see how angles can be defined by them.

From the Pythagorean theorem we showed that in any right triangle, 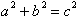. The equation :

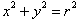
Is therefore the set of all points a distance r from the origin, from the distance formula which is based on the Pythagorean theorem. The important point to realize here is that the co-ordinates of each point on the circle gives us the dimension of a unique right-triangle with base, x , height, y and hypotenuse r. Each point satisfies the Pythagorean theorem for right triangles, 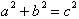; though the radius or hypotenuse remains fixed, the x and y.s can take on infinite values.

To visualize these concepts, the Graph of the circle

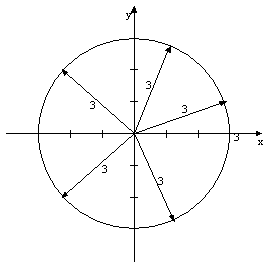
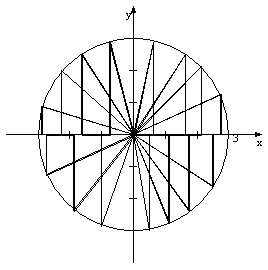
Let us now look at how to define an angle in terms of the circle. An angle in all simplicity is the measurement of rotation between two intersecting lines. This rotation can be expressed in terms of the arc length of the circle. If you follow the path of a point at (3,0) to (0,3) along the arc of the circle then you will notice that the radius drawn to each point on the path will increase at a steady rate.

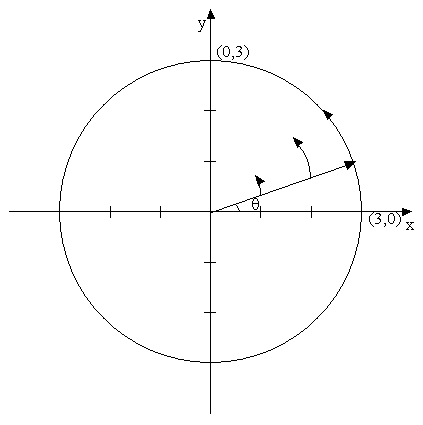
You can notice two points here. First the circumference of this circle is given by the formula:

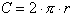
This tells us the total arc length of this circle is just 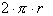, where r is the radius. Now if we define there to be 360 degrees in a circle, what this means is that a line that rotates a full circle to return to its original position will have covered 360 degrees ( a completely arbitrary number). Since degrees are a measurement of an angle, or the amount a line or r in the graph has rotated then we must figure out some method of relating the arc length, a measurement of rotation to degrees.

If we define there to be 360 degrees in one full rotation the ratio of some number of degrees q to 360 degrees must equal the ration of the arc length covered to the  total arc length of the circle.

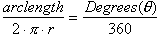
Multiplying terms out to solve for degrees gives us:

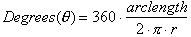
There is still one thing left, this definition of degrees is entirely dependent on the radius of the circle. If you recall from our discussion of the relativity of size in mathematics as being meaningless without reference to something else, then theoretically 30 degrees should be independent of the size of the circle it is measured in. To account for this we introduce an important new concept, the radian. The radian is a relativistic measurement for arc length that gives us the arc length measurement in terms of the radius of the circle.

For example in a circle of radius 2, the circumference is 4 p. An arc length of 2 radians is then just 4 units long or twice the radius. Since the circumference of the circle is directly related to its radius then an arc length in radians will always have the same relative size to its circle, regardless of the size of the circle. This probably sounds more confusing than it really is, but this is all because we are looking for a way to define degrees in terms of arc length. If we replace arc length with radians*r, where r represents the constant radius and radians is any number which could be a fraction we get:

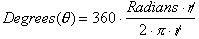
This important equation now tells us how to define an angle in terms of the radian measurement of an arc length, measured in radians. We can re-write it as:

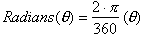
The important point to realize throughout this discussion of what an angle is, is that angles can only be first defined in terms of arc length rotations between two lines measured in radians. Having established radians, only then can we also use degrees, which is just another unit of measurement of angles entirely based on radians. Instead of calling an angle .86 radians we can say 60 degrees:

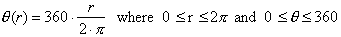
Degrees are directly related to radians, and are more often used when there is no reference circle to define an angle easily.

Let us now return to our discussion of circles. Having established just what an angle refers to conceptually we now need to define an angle mathematically. We shall select for our study a circle of radius one, which is often called the unit-circle, for reasons soon to be seen. If we draw a small triangle in the unit-circle we can see that:

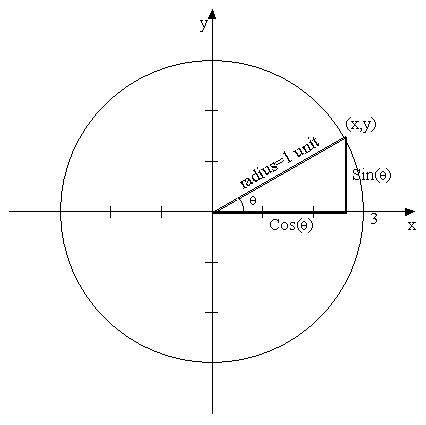
In such a triangle

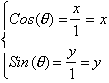
What this means is that for any point 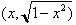on the unit circle, the Sine of the arc length measured from (0,) to (x, y) will be the y value of that particular arc length. For example:

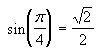
In terms of triangles and degrees, this says that the ratio of the opposite side to the hypotenuse of a 45 degree angle is just 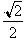. It is extremely important to forget about triangles and degrees for the moment but just concentrate on circles and arc lengths which are both mathematically defined shapes. In terms of the unit circle whose the angle measurement 45 degrees is expressed in terms of the arc length of a circle whose radius is 1. pi/4 then refers to an arc length of 0.78 radii.

Error in picture below, it should say 0.78, not 1.56

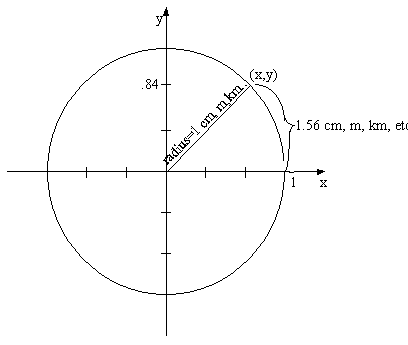
We are now ready to define the Sine function as that function that outputs the y-value  for an inputted arc length of a unit circle. The cosine functions gives us the x-value  for that same arc length. It is here where the difficulty arises. We need to find a way of expressing the arc length of a circle a unit circle in terms of x and y. By being able to calculate the arc-length in terms of x and y values, the Sines and Cosines will just be the x and y values of the point until which we are calculating the arc length. Therefore the Sine function is really an arc length function as we shall soon see.

To begin let us recall our formula for calculating the length of curves of graphs of equations. It was defined as the following differential that gives the length of a hypotenuse used to approximate the graph over a small interval of x.

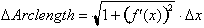
Integrating it to find the total arc length.

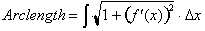
For example the length from 0 to 1 of the following graph of y= 5x is:

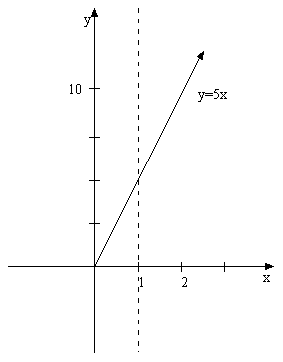
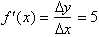
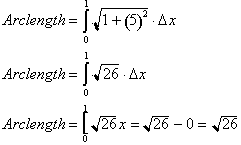
The length of the graph from 0 to 1 therefore has length 5.22.

Relating this to our study of the circle, the arc length can be expressed as follows:

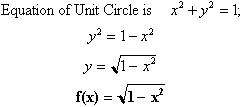
The derivative of this function for a circle is:

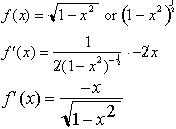
The arc length from zero to a where, a is less than or equal to 1 is:

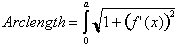
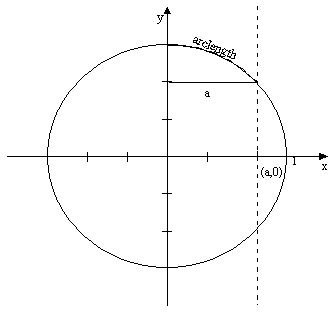
In the circle this translates to:

There are two important points to understand here. First for any 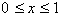inputted the output will be an arc length measured in radians since we are dealing with the unit circle. For example if I were to evaluate the integral from x=0 to x=1 I should get 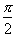or 1.57 radii. The second point to keep in mind is that 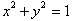is the same as 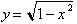and 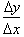is therefore

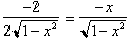
Returning to our integral we have:

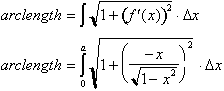
Simplifying the integral:

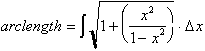
The expression in the radical, 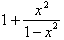can be further reduced to 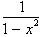by adding the two fractions:

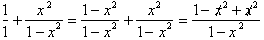
This now gives us:

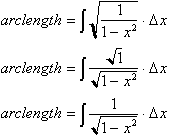
The question now arises, . how do we interpret this or relate it to the Sine function. To answer this let us study the graph of the circle once more. Since we commonly measure arc lengths in radians or degrees beginning at (1,0) it will require a moments thought to realize that now we are measuring angles from (0,1).

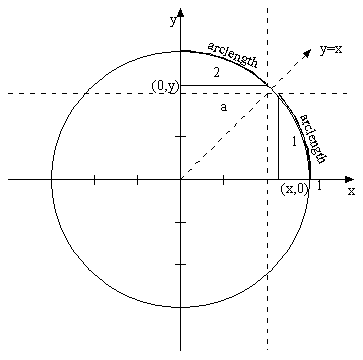
First take a look at section 1. It represents the way we initially defined the Sine Function, where Sine( arc length) = y. Now examine section 2. It is exactly the same as section 1 excepts instead of y we have x. The sections are identical because the graph of a circle is symmetric about the line y= x. We can therefore define the Sine function as follows.

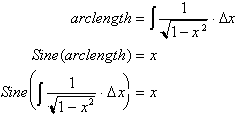
Since x is our output and not our input here, we need to find a better way of defining the Sine function. If you recall from our study of inverse functions, we saw that the inverse function always yields x when inputted in the original function since a function and its inverse were essentially the same function except that the x and y were switched around, and the two functions were then graphed in the same x-y plane. For example if we had 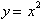then its inverse was found by replacing y with x to get 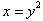or 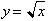. 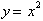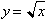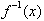Since any point (x, y) on the graph of has a corresponding point on (y, x) on the graph of its inverse; then inputing y values from in 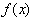would output x values. For example:

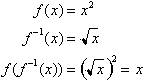
This may sound more complicated then it really is but we can now conclude that since the Sine of the arc length integral outputs x, then that integral is the inverse of the Sine function:

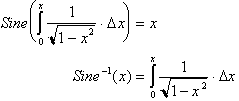
The inverse sine function is commonly called the arcsine function which is analogous to asking what angle or arc length has sin x?

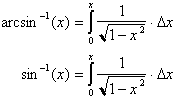
At this point is important to stop thinking about angles, degrees, and triangles. What is essential now are circles and arc lengths measured in radians. The Sine function, mathematically speaking is then just the function gives the corresponding x value of an arc length measured from to 0 to x on the circle. The inverse sine of a number x is then just the arc length from 0 to x on the graph of a circle. This is all it is, nothing more, nothing less. The inverse sine function is therefore our most important function since it serves as the base for calculating arc lengths for any

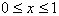
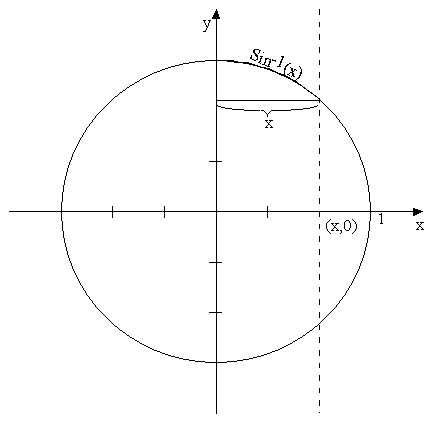
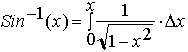
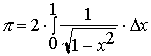
This concludes our definition of the Sine function as mathematical function to express the arc length of a unit circle, or any circle. You can already begin to see the problems we will encounter in integrating it since the arc length approach infinity towards x=1.