CHAPTER 5
Chapter 5 - Differentiating Functions
Section 5.4 - Differentiating Functions of any power N
We have proven that if
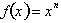then
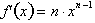for
n equal to a positive integer, i.e. 1,
2, 3, 4 etc. What if n were a
fraction such that
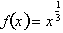. As we shall prove,
the derivative of any function of x of the form
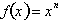is always
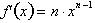where n is any real number, positive, negative, or fraction. This is no
coincidence but is because of the way exponents are defined as a continuous
operation for any n. Let us consider
the first case of
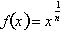, where n is any positive integer and 1/n is a fraction.
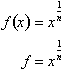
Raising both
sides to the n’th power:
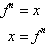
Differentiating x, with respect to f yields:
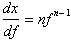
Taking the
reciprocal of the function:
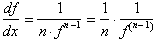
From the
definition of the function, we know that
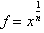. Making this substitution:
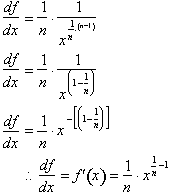
This concludes the proof that if
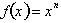then
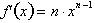, for any positive n,
integer or fraction. We will prove it also holds true for n as a negative
number.
We can use the product rule to prove
that the derivative of
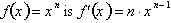for all n, negative real numbers also. Consider the function:
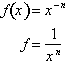
Multiplying both
sides by
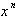yields:
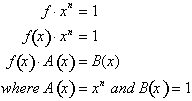
The left side of the equation
represents a product of two functions, f and
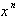, and the right side is a constant function,
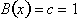. Since both functions are equal to each then their
derivatives must be equal. Using the
product rule to differentiate the left side with respect to x results in:
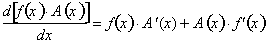
Similarly,
differentiating the right side with respect to x yields:
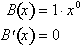
Setting the
derivatives of the left and right side equal to each other:
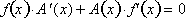
Remember that:
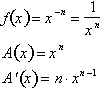
Making the
required substitutions:
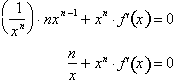
We can now solve
for
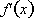
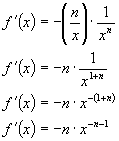
Therefore if
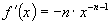, where -n is a negative integer. We have
proven that if
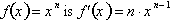for positive real
numbers and negative integers. What remains is to prove it true for negative
fractional powers as well. To do this let,
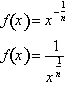
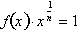. Differentiating both sides with respect to x yields:
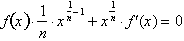
Substituting
known values for f(x) and solving for
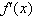gives us:
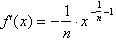
Thus if
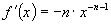for any n,
positive or negative real number. This is true because of the way exponents are
defined as a uniform operation for any n.
The purpose of going through all the proofs for the different cases of n was to give you a better understanding
of how to differentiate functions of x with
respect to x.
Next section ->
Section 5.5 - Differentiating Functions of Functions
