Chapter 8 - Understanding the Derivative
Chapter 8 - Understanding the Derivative
Section 8.3 - Systematic use of the Derivatives
We shall now look at a systematic
and orderly way of interpreting our knowledge of a function’s first and second
derivative. Before continuing let us return to the concept of the inflection
point. An inflection point is a point on the graph where the concavity shifts
from being concave up to concave down or vice-versa. Since a negative second
derivative reflects a concave down graph while a positive second derivative
represents a concave up graph then inflection point occur where,
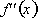is equal to zero. Note that inflection points do not have to
exist at equilibrium points. For example in the graph of
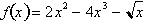, the derivatives
value at the inflection point (x=0.45) is not equal to zero.
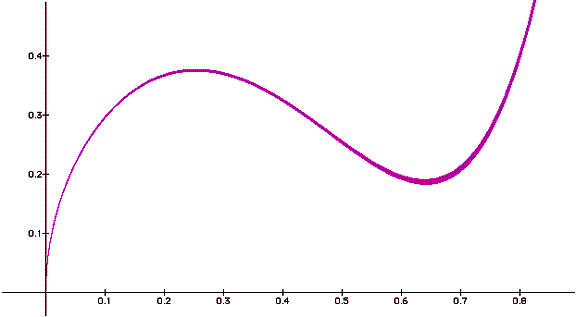
In some rare cases, the value of the
derivatives can be of the same sign before and after an equilibrium point. In
such cases the graph of the function,
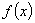has to be determined
by carefully looking at both the functions first and second derivative. To make
this analysis simpler, let us go through a step by step process for predicting
the behavior of
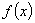, using only
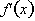and
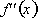
To begin drawing f(x), first find
maximum and minimum values by setting f’(x) equal to zero, and solving for x.
Next find inflection points by setting f’’(x) = 0 and solving for x. Then plot
two number lines for both f’(x) and
f’’(x) with plus and minus signs to indicate where they are positive and
negative. First look at f’(x) to understand where the graph is increasing or
decreasing. Next look at f’’(x) to find out how the graph is increasing or
decreasing, concave up or down. The number line for the example is:
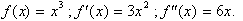
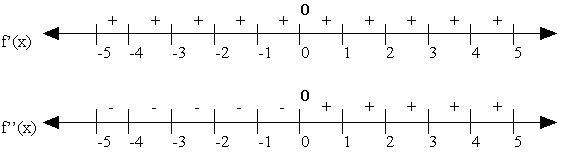
Having drawn this important number
line, how do we make interpret it. Remember positive rate of change implies
that
is increasing while
the reverse is true for negative rate of change. Similarly a positive second
derivative implies that the graph is concave up while negative values represent
concave down. Then use equilibrium points to draw the graph through them.
Next section ->
The Derivative and its Approximations
