CHAPTER 3
Chapter 3 - The Mathematical function and its Graph
CHAPTER 3
Section 3.4 The Mathematical Function
The mathematical function expresses the relationship
between a situation and the conditions that define it. The form of the
mathematical function is thus:
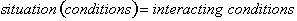
This is read as, a situation
is a function of certain conditions. The conditions are called dimensions.
For example, consider the mathematical function for calculating the force
acting on a body of mass, m.
Force = Mass * Acceleration
The force on a body is a
situation defined by two conditions, mass and acceleration. In a closed system
, the force acting on an accelerating mass, is the product of the mass and its
acceleration. Thus, force is a function of two dimensions, mass and acceleration
while force is the third dimension
dependent on m and a of the system. Therefore force is called the dependent dimension
while mass and
acceleration are the independent dimensions that together define the dependent
dimension. The dependent dimension, F, is placed outside the brackets, while the independent
dimension are inside the brackets. Remember . the language of mathematics is as concise
as possible. The function is more commonly written as:
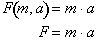
For example, the force required to accelerate a 5 kg object at 3
meters per second per second ( acceleration is by definition the change
in speed per unit time ) is 15 N,
where N represents Newtons, the unit of measurement representing force:
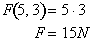
One is free to use any value
of m and a to calculate the corresponding force. For this reason, m and a are
called independent dimensions, while F is the dependent dimension defined by
them. Note that m and a must come from the same
system, and the calculated force refers to that situation only.
What if I were given the acceleration of a body and the
force acting on it and wanted to calculate its mass? In other words, given F
and a, what is m? This is done by solving the force function for m or:
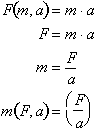
Therefore, mass as a
function of its acceleration and the force acting on it, is the force divided
by the acceleration. Here mass is the dependent dimension dependent on force
and acceleration. Once again, the three dimensions, mass, force, and
acceleration must all refer to the same situation.
It is not uncommon in engineering to encounter twelve to
fifteen dimensional functions. For example, consider the five dimensional
function for calculating the elongation of a cable being stretched with some
tensional force.
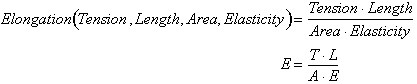
The total elongation of the cable is dependent on four conditions.
The tension acting on it, its length, the cross-sectional area, and a
material property called elasticity. The point to understand is that the
n'th condition is entirely dependent on the other ( n - 1 ) independent
conditions. The ( n - 1 ) independent dimensions represent a set of fixed or
constant conditions that together define the n'th dimension .
Questions
- The distance covered by a falling object near the surface of
the earth is given by:
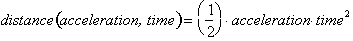
Simplify this function using d for distance, t for time etc.
The
acceleration can assumed to be a constant 9.8 m/s/s. Substitute this constant
into the function and write the expression for distance as a function of time.
To find approximately how tall you are, drop an object from the top of your head
and using a stopwatch, find the time taken for it to hit the ground. Substitute
this time into the distance function just derived. The answer should be close
to your height. Try this at least ten times to get a close approximation.
Calculate your height in feet using the following function:
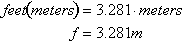
You might think your answer will be different
if you had dropped a metal object , paper or a balloon. You are correct, however,
it
is due to air resistance which is a function of amount of surface area exposed
to the direction of travel. So you should get the same answer no matter how heavy your
object is as long as it is relatively immune to air resistance.