Chapter 23 - More on Taylor Series

In this second chapter on Taylor Series, we will be studying the case where the n.th derivative of an infinitely differentiable function, does not go to zero. In such cases we therefore have to restrict our values of x., such that for these values the series does converge and not diverge. We will also take a look at the series for the Exponential and Sine function.

          Let us begin with a look once again at the series for the infinitely differentiable function, the square root of x. The theories that we are to develop will hold true for any function raised to a positive or negative fractional exponent.

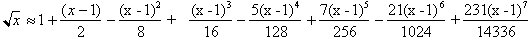
Remember we let a=1 to find the square root of any number x. Take a close look at the fractions preceding each term:

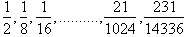
It seems that they are slowly going to zero, but now look at the terms of the Taylor Series:

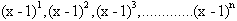
Since each term represents a power of some number (x-1), then we can conclude that if this number is greater than 1, then each term in the series will get larger and larger and approach infinity, in the infinite term.

However if the absolute value of (x-1) were less than 1, then as the number of terms in the series increased, the value of each term will decrease. Therefore we can say that the following series is only valid for:

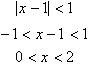
This tells us that for x in this range of values, the infinite term will go to zero and the series will converge. Remember, the more times you multiply a fraction by itself, the smaller it becomes.

Now that we have defined the series for a certain range of numbers then we can extend this range to include all the real numbers. For example we can find the square root of any fraction 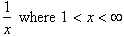. This means we can find the square root of any number, greater than 2, by taking the reciprocal of its square root. If we had to find the 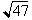, then we just rewrite it as 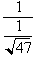. Since 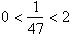then we just find the square root of 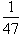by letting x= 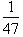, then taking the reciprocal of this value.

Now let us move on to finding Taylor Series for the exponential and Complex Sine Function. The Taylor series for 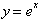>can be easily found since its n derivatives are all the same, 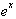. The series is then:

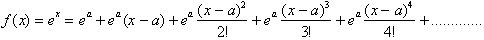
The easiest value to choose for a is 0 since

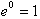
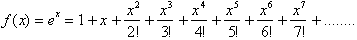
Since the limit as n goes to infinity of 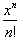is zero, regardless of what value x is, then the series is valid for any value of.
          Letting x=1 and using only the first eight terms gives us the value for e:

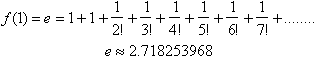
The calculator value for e is 2.718281828 which corresponds to an error of less than .001 % using only eight terms. The more terms used the more accurate your answer will be.

Now that we have found the series for 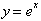>we can find the Taylor series for y= ln (x), which is also an infinitely differentiable function. Fist let is find its n. derivatives:

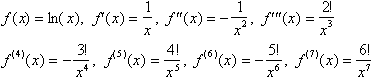
Using the first seven derivatives we write the following Taylor series:

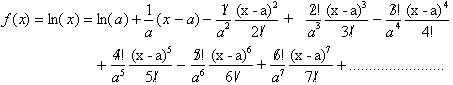
Letting a equal 1:

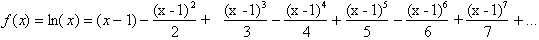
There is one small problem here. Though the Natural Log of x is defined for all values of x greater than zero, the Taylor series on the other hand is only valid for 1<x<2. If x were three for example, the series on the right would diverge as each term, 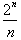will get larger and larger.

In an infinitely differentiable function as in 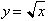, we assumed that the last term in:

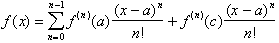
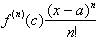
went to zero as n went to infinity. This was based on the fact that

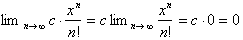
However in the case of the series for the natural log of x, the last few terms become:

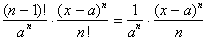
Taking the limit as n goes to infinity:

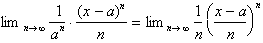
The limit of this function clearly goes to infinity as long as the absolute value of 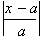is greater than 1. Conversely if 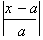is less than 1 or 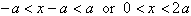, then the last term will go to zero and the Taylor Series will hold true. By making the modification to the Taylor Series for ln(x), the series will converge for 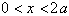. Since a =1 the series converges for:

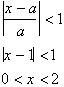
Hence the series:

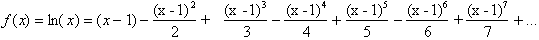
is valid for x between 0 and 2. Despite the restricted value of x, we are still able to calculate the ln (x) for any x, by just taking reciprocal values. If we wanted to find the ln (40), 40>2 we would have to calculate 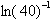which equals

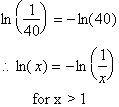
The Taylor Series for Sin(x) and Cos(x) are also quite easy to find. Since we know the derivative of Sin(x) is Cos(x) and Cos(x) is -Sin(x) and we can evaluate these functions at a=0,  as Sin(0)=0 and Cos(0)=1, the Taylor Series are as follows. First find the first few derivatives.

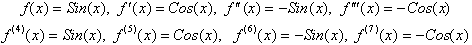
Using this to write the Taylor Series for the first eight terms is:

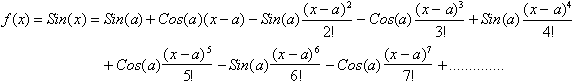
Letting a=1

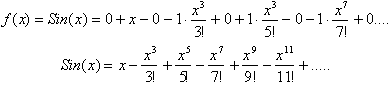
Since the limit the infinite term in this series goes to zero as n goes to infinity, then the series is convergent for all values of x.

Differentiating the series gives us the Taylor series for Cos(x):

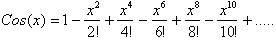
This solution is remarkable .It allows us to define the Sine and Cosine functions mathematically in terms of an infinite series. You might be wondering how the series is define for any arc length, 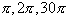etc.

From the graph of the circle it is clear that its arc length is continuous and passes throughout the same point infinite times as it completes its rounds. For this reason our integral for the inverse sine function could only be solved using imaginary numbers. Our study of the Sine function began with simplicity, rose to reason, climaxed in the abstract, fell into the imaginary, and now ends in perfection.

Our study of Taylor Series showed us how by integrating a function 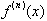, n times, we were able to express f(x) in terms of its n derivatives evaluated at a point a with the last terms being evaluated at some point c, between a and x. The series took the form:

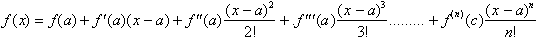
Taylor.s Theorem thus states:

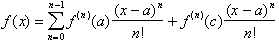
The important point to realize here is that n stands for an integer, such that a finite differentiable function can be expressed as a series of its n derivatives evaluated at some point a. The last term, 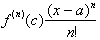can be found regardless of the value of c sine the last derivative of a finite differentiable function is always a constant.

As we saw, expressing finite differentiable functions in terms of a series of powers of x turned out to be impractical. It is here where we saw the value of extending Taylor.s theorem to infinitely differentiable functions.  This would mean we would have an infinite series with infinite derivatives. The only way to prove that such a series could be written and would hold true for any value of x was by taking the limit of:

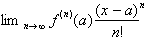
If the limit was zero then we know that 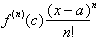, or the last term of the series also goes to zero and therefore the series converges for al values of x . If this limit did not go to zero then we had to modify or restrict the values of such that the series would converge for those values of x. We could then extend this interval for all real numbers.