Preface
The purpose of this book is to
present mathematics as the science of deductive reasoning and not as the art of
manipulation.
Unfortunately, many students feel mathematics is incomprehensible and
is riddled with
complex and abstract jargon.
My goal is to impose a lasting
understanding of and appreciation for calculus on the student.
Unfortunately, students are rarely given any example of practical applications.
The curriculum's idea of exercises is nothing more than sheer
number-crunching and manipulation of variables. The entire underlying
principle of order and beauty upon which calculus is based, is
neglected. The problems never call upon the student's ability to think
logically. Rather, they require no more than time and persistence, to
allow the trial and error method to succeed.
It is clear that the above scenario
leaves the student with no more than two options. One, they can burden their
mind out in trying to make sense of this mysterious science, where
theorems appear out of nowhere and seem to have no connection with previously
learned material. Or second, they can choose to memorize. Without a doubt,
the majority of students will opt for the latter. Not only is it less
time-consuming, but it also yields the correct answer!
One may argue that it is not important for students to understand
what they are learning. It is especially disheartening to see everyone around
you not care about understanding knowledge.
One should just learn to accept and
tolerate it , rather than criticize and feel bad about it. Such is the
way of the world. If you want to create a system you need to have the
understanding, but to run a system ( which most people do ), just cook
book procedures are all you need to know.
The over-emphasis on the calculator
and foremostly the computer is yet another point of confusion for the student.
The computer is only a time-saving machine whose usefulness depends
on the knowledge of the user. I do admit the computer is a
remarkable machine, yet it is this fascination that gives students a false
sense of what they are doing. The confidence gained from all the correct
answers leads to an inseparable dependence where the student is
absolutely helpless without it.
It is all these shortcomings I set out to correct in writing my book.
My book is intended to give the student an
understanding of what calculus is truly about. Only by explaining where
something has come from will I be able to show where it is going. It does not
take more intelligence than that of a parrot to be able to go through a list of
theorems and equations; but only when one understands their origins can one
correctly and confidently apply them in the real world.
I assume absolutely nothing and
neither do I take anything for granted. Each chapter has a definite beginning,
followed by logical, elegant and clear proofs, concluded with a brief summary
that ties everything together. My only reference has been reason and if you
could find just three lines that remotely resemble the lines from any other
book, I would feel greatly distressed.
Throughout the textbook I constantly
refer to science and engineering. The purpose of this to show how the scientific
method applies to all disciplines and to understand that mathematics is an
expression of one’s observations and hypothesis. I do not overdose the student
with series of real-world applications where calculus is applied. Doing so
would only succeed in showing that
calculus and real-world applications are linked together by chance alone. My
goal is to present mathematics through science. Therefore an emphasis is placed
on mastering the scientific method of analysis through understanding the necessary
concepts of differential and integral calculus.
My book begins with a brief yet
important review of the number system, laws of arithmetic, and some algebra. I
have used simple pictures to show the student these fundamental concepts and
operations. My definition of a number culminates with a philosophical look at
the difference between actions and objects and then explains how a number can
represent either attribute. There are no rigorous definition muddled with Greek
language and abstract symbols.
The goal is for the student to
visually understand the operations he or she takes for granted though uses so
extensively. It is not obvious why multiplication and division dominate most
fundamental equations from engineering to biology. For example many students
can not explain conceptually the difference between 2+2 and 2 X 2, much less
why a fraction times another fraction results in smaller number. This is due to
the student’s inability to relate the concept of the number with multiplication. The chapter I have
written reduces all the operations of arithmetic with the philosophical definition
I have given to the number as an independent entity.
After this chapter I begin my
in-depth study of calculus with an introduction to the function, giving full
and complete definitions that center on perceiving it as a mathematical
relationship. I introduce the concept of dimension to show how a function
defines a situation in terms of its interacting conditions or dimensions.
I then show how it is possible to
graph a function in a two-dimensional system using the idea of the independent
and dependent variable. From plotting a few points to plotting more points I
intuitively show the behavior of a function is only as accurate as the numbers of
points it has been evaluated at. Once again it is not obvious how a function
can be graphed as continuous changing line. I then give a short proof, using
the idea of a small change in x producing a small change in f(x)
to explain how the graph of the function is the continuous
line drawn through these points. This is all done with graphical examples
followed by a complete explanation of what exactly is going on.
Having completed the chapter on functions and their graphs, I begin
a thorough immersion into the analysis of the function and its graph.
Beginning with a few pages just on the definition of rate of change, I
move on to a long study of the graph of a function that is not constant.
Of course I do not begin with the assumption that the slope is not
constant. I divide the graph over an interval into small intervals
Dx, over which the graph
will be analyzed independently. Again using the idea of slopes I
introduce the terms average and approximate rates of change. It is here
where I explain the equation for the average rate of change through any
two points on the graph:
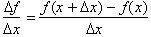
Having established this equation I then proceed to analyze the graph
in a more complete way by breaking it up into intervals of value
D x equal to a small
number. The goal is for the student to understand that we are now looking
for a way of defining the instantaneous rate of change of the function.
From there I develop the concept of taking the limit and showing exactly
what is meant by tangent to a graph. Building upon the slope equation and
my definition of the graph of a function as a line connecting a set of
points I show what exactly is meant by having a unique line through “one”
point. Once again I use clear and simple examples that contain a
minimum of notation and focus on understanding the relation between
instantaneous rate of change and calculus.
I then go on to derive the normal
rules for differentiation, clearly explaining each step in the derivations. I
take considerable time with the chain rule which derives itself from the
definition of a function and the rules for differentiating them.
From there I move on to the graphical interpretation of the
derivative and the second derivative. As always I go through a clear and
complete explanations of concavity and by assuming
nothing. The underlying goal of this chapter is for the student to
understand the relationship between the function and its derivative.
This is done by emphasizing that the behavior of a function can be entirely predicted just by
studying its derivative, f’(x).
Having developed this link between
function and derivative I take a more numerical and thorough look at how the
derivative alone can be used to accurately graph the original functions. First
I show how the equation:
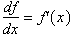
can be thought
of as
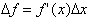 I take considerable time explaining the difference between the discrete
I take considerable time explaining the difference between the discrete
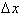 and the differential . Using this new equation I explain linearization and errors.
In the next section of this chapter I introduce the process of integration. By
taking a graph
and the differential . Using this new equation I explain linearization and errors.
In the next section of this chapter I introduce the process of integration. By
taking a graph
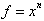 and breaking it up into four continuous sub-intervals I show how the exact
change in the function, f, over the
entire interval can be found by evaluating the
f’(x) Dx
over each sub-interval D
x
and then summing up the delta x
f . In the discussion it becomes rather obvious how the exact
d
f’s of the graph can only be found by letting our D
x go to a
smaller number and summing up the many
f’(x) D
x
over the
interval. In explaining all this I only use two new symbols:
and breaking it up into four continuous sub-intervals I show how the exact
change in the function, f, over the
entire interval can be found by evaluating the
f’(x) Dx
over each sub-interval D
x
and then summing up the delta x
f . In the discussion it becomes rather obvious how the exact
d
f’s of the graph can only be found by letting our D
x go to a
smaller number and summing up the many
f’(x) D
x
over the
interval. In explaining all this I only use two new symbols:
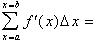
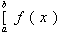
It is in my highly theoretical
chapter on Integration do I delve into the meaning of this equation and
introduce the integral sign between the two symbols. What I do in this chapter
is basically undo all that I did with the derivative. Throughout my discussion
of the derivative I show it as a subtracting and dividing process. In
explaining integration I show it as a multiplying and adding process or the
reverse of differentiation. The emphasis is placed on understanding the
relation the derivative has to its integral in terms of the net change in a
function f(x) from a to b can be found by evaluating the derivative times a
small D
x and summing up these values
from a to b. I show intuitively how the error gets less and less as D
x gets smaller by using areas. By presenting different
simple proofs for the Fundamental theorem of calculus, there should be little
doubt in the students mind as to what integration means and more importantly how
it relates to concept of differential change.
The next chapter I go through a
series of geometric applications from areas to arc length. As an Engineer I
have seen that students are generally completely helpless when it comes to
setting up integrals. This is entirely due to the fact that the student has no
idea what it means to integrate a function although they are more than capable
of integrating some of the most awkward looking functions. What this chapter
does is draw the bridge between the theory in the previous chapter and the
practical applications in the following chapter. Even though the student
understands integration, applying it requires yet another theoretical chapter.
The transition from
f, x, F, M, P etc.. to
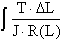 ( the integral for
finding the total angle of twist of a rod, length L, of varying radius with J
as the polar moment of inertia subjected by a twisting torsion force, T) appear to have little to do with each other
except that they are evaluated the same way.
( the integral for
finding the total angle of twist of a rod, length L, of varying radius with J
as the polar moment of inertia subjected by a twisting torsion force, T) appear to have little to do with each other
except that they are evaluated the same way.
In going through the geometric applications I leave behind all the
x’s, f’s and f(x)'s and replace them with their geometric equivalents of
length, l, width, w, and height, h. In
order to understand how to set up integral I use the concept of a independent
and dependent variable to explain when one constant is changing with respect to
another constant a differential needs to be written. I do not delve too much into this theory of writing
differentials as I leave it to the next chapter where identifying the
differential is not a simple matter of
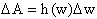 .
I concentrate on understanding the integral as a three step
process of summation, integration and then evaluation. What is important is the
method as the previous chapter already explained how these processes are all
related.
.
I concentrate on understanding the integral as a three step
process of summation, integration and then evaluation. What is important is the
method as the previous chapter already explained how these processes are all
related.
It is in the final chapter on
applications of integration that it becomes necessary to develop a consistent
theory of integration that can be applied to any problem from engineering to
economics. I further develop the idea of a constant being expressed as a
function of another constant and then explaining how to identify the
independent variable in the equation. I present a logical and reasonable
algorithm for setting up integrals in problems.
This is perhaps the most important
chapter in my book as its goal is to reconcile the theory of function, change,
differentiation and integration all into one clear and concise method. This is
really what calculus is all about. Modern textbooks devote most of their time
to evaluating integrals while they completely disregard the numerous steps that
must be taken before an integral can be set up and evaluated. A student must be
able to understand how to set up an integral in a practical situation be it
from electromagnetic forces to dynamic response of a skyscraper during an
earthquake. Calculus is an utterly
useless tool without this fundamental understanding of what integration is all
about as the student will be able to play with calculus but he or she will
never know how to use it.
This ends my text-book on calculus.
My book is intended to offer an introduction to calculus for College or High-School.
The course may be completed in either one semester or one year, depending how
in depth the instructor is prepared to go. Throughout this Preface or
introduction, I have constantly been referring to my complete discussions and
explanations that are unlike the nonsense that accompanies theorems and
concepts in other books. It is difficult to explain how exactly it is different
for that would require my re-writing the book in these
opening lines. I can
assure you that what awaits you is something unlike anything you have read and
studied before.
More than 85% of the work is original and entirely conceived
using the power of reason and logic. The remaining 15% is material that
is covered in most every text. Though my presentation of such material has
resemblance of form, in terms of content it is considerably different. Other
books present a puzzle whereas I have taken the time to complete that puzzle
not to mention adding further observations along the way to help strengthen the
student's understanding.
It is therefore no overstatement to
say that the entire book is unique and has almost no connection to the modern
textbook. The only way to judge the validity of this statement is to continue
on and read it. I am certain what you will learn will fascinate you.