CHAPTER 10
Chapter 10 - Theory of Integration
The goal of this chapter is to undo
all that has been done in the previous chapters on differentiation. We saw
how
the derivative can be used to approximate the anti-derivative, but how do
we
use it to give us the exact behavior of its anti-derivative?
Differentiation involves two main
operations. The first is subtraction or letting a change in x,
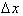 get smaller. The
second operation is division to calculate the relative change of the
dependent
variable, f with respect to the independent variable, x. Therefore, the
focus
of this chapter will be on summation and multiplication.
get smaller. The
second operation is division to calculate the relative change of the
dependent
variable, f with respect to the independent variable, x. Therefore, the
focus
of this chapter will be on summation and multiplication.
To begin our study, let us look at
the definition of the derivative of a function,
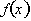
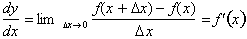
What this definition does is analyze
a changing function over an infinitely small interval to calculate the
rate of
change of the function at that instant. By letting
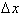 go to zero, the terms
interval and point become synonymous such that the derivative gives the
rate
of change at any point x. If we multiply both sides of the equation by dx
,where
go to zero, the terms
interval and point become synonymous such that the derivative gives the
rate
of change at any point x. If we multiply both sides of the equation by dx
,where
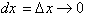 we get:
we get:
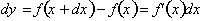
We can calculate the approximate
change in the function,
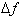 by replacing the
infinitesimal dx with a discrete
by replacing the
infinitesimal dx with a discrete
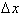
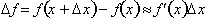
The answer is only an approximation
because the equation assumes that the rate of change or derivative is
constant
over the interval
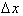 . For example consider the following linear function:
. For example consider the following linear function:
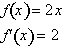
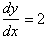 or is a constant. At
any point on the graph of
or is a constant. At
any point on the graph of
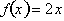 , the rate of change is reflected by the constant steepness
of the graph. Now let me pose a simple question. How much does the
function,
, the rate of change is reflected by the constant steepness
of the graph. Now let me pose a simple question. How much does the
function,
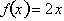 , change when x goes from 0 to 4? By evaluating
, change when x goes from 0 to 4? By evaluating
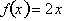 at 0 and 4 we get:
at 0 and 4 we get:
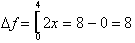
The new symbol [ means to evaluate the function at the two values
specified on the symbol and subtract the difference.
When x changes from 0 to 4, the dependent variable, f, changes by
8. How
else could we arrive at the same answer? From the definition of the
derivative
we know that:
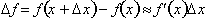
Over an interval
Δx,
the change in f(x), can be approximated by evaluating
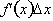 for the interval. Let
us see how this applies to the function we were studying. We have shown
that as
x changes from 0 to 4, f changed from 0 to 8. Now let us find the same
answer
using the above equation:
for the interval. Let
us see how this applies to the function we were studying. We have shown
that as
x changes from 0 to 4, f changed from 0 to 8. Now let us find the same
answer
using the above equation:
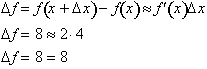
The answer obtained from the
derivative is exact because the
rate
of change of the function is constant over the discrete interval,
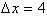
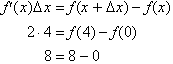
But what if the derivative is
not a constant but varies with x? As we shall soon prove, the total change
of a
function f(x) from x = a to x = b is found by taking the infinite sum of
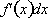 from a to b where
each
from a to b where
each
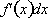 gives an
infinitely small change in the
function, df, over the infinitely
small
interval, dx.
gives an
infinitely small change in the
function, df, over the infinitely
small
interval, dx.
Let us look at a function whose
derivative varies with x:
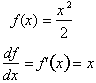
As x changes the rate of change of
f(x) increases. We can begin by asking ourselves what is the change in
f(x), when x changes from 0 to 8?
In
the graph this translates to:
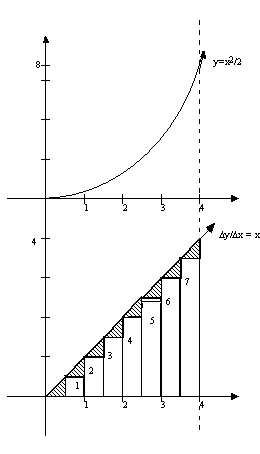
For the function,
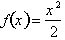 , when
Δx
goes from 0 to 8,
Δf
is
given by the equation:
, when
Δx
goes from 0 to 8,
Δf
is
given by the equation:
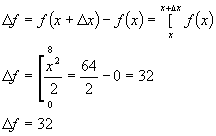
How else could we
calculate the change in f? From the derivative we know that:
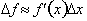
Since the derivative of
the function changes with x, then we need to evaluate the above equation
over
small intervals of
Δx
to
get an accurate answer. Remember the rate of change of f(x) is changing
and is
not constant over a discrete interval,
Δx.
By breaking up the
derivative,
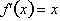 into 8 intervals of
Δx = 1, we
can approximate the change in of
into 8 intervals of
Δx = 1, we
can approximate the change in of
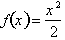 from x = 0 to
x = 8 by using the derivative only. A small
Δf of the graph is found by evaluating
from x = 0 to
x = 8 by using the derivative only. A small
Δf of the graph is found by evaluating
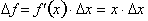 over each interval,
over each interval,
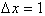
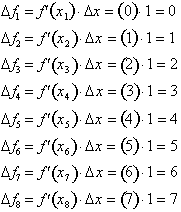
The net change in f(x)
is found by summing up the individual approximations of
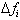 , for each interval.
, for each interval.
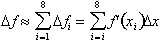
Substituting known values in:
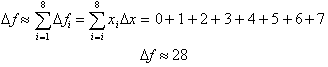
Adding up the
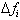 , we get 28. This corresponds to an error of 4 since we
calculated the actual
Δf
of f(x) to be 32 as:
, we get 28. This corresponds to an error of 4 since we
calculated the actual
Δf
of f(x) to be 32 as:
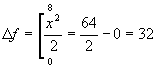
To approximate this
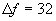 we evaluated the
derivative,
we evaluated the
derivative,
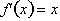 over small
sub-intervals to calculate the net change in the function,
over small
sub-intervals to calculate the net change in the function,
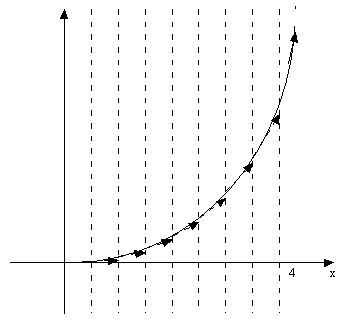
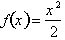 . Relating the instantaneous rate of change to the slope of the tangent
is:
. Relating the instantaneous rate of change to the slope of the tangent
is:
By evaluating the
derivative over each interval
Δx
we got the approximate
Δf
of
f(x) over that interval only.
How
could we get a more accurate result? The solution is to further divide the
interval into a smaller
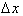 , such that the derivative is assumed to be constant over the infinitely small
interval. If we let
, such that the derivative is assumed to be constant over the infinitely small
interval. If we let
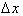 equal 0.5, we will
have sixteen intervals over which we can calculate the
equal 0.5, we will
have sixteen intervals over which we can calculate the
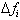
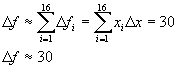
You can clearly see that
by further reducing the interval, the error is difference between the
approximate and actual
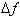 is very small. By using sixteen intervals, we reduced the error from 4 to 2. We can
go on to conclude that as the interval,
is very small. By using sixteen intervals, we reduced the error from 4 to 2. We can
go on to conclude that as the interval,
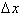 , goes to zero, then the net change in f(x), will correspond
exactly to the infinite sum of the derivatives evaluated over each
interval,
, goes to zero, then the net change in f(x), will correspond
exactly to the infinite sum of the derivatives evaluated over each
interval,
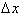
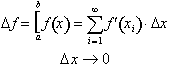
Thus the net change in a
function from a to b is exactly equal to the infinite sum of its
derivative
evaluated over an infinitely small interval,
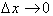 One argument
against such a conclusion is that as
One argument
against such a conclusion is that as
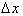 decreases, the error
gets smaller for each individual interval however the total error remains
the
same. This is because as
decreases, the error
gets smaller for each individual interval however the total error remains
the
same. This is because as
 , we are adding up an infinite sum of small errors as opposed
to a discrete sum of 8 or 10 for example. We have shown intuitively that
this
does not happen, but how can we
prove
it?
, we are adding up an infinite sum of small errors as opposed
to a discrete sum of 8 or 10 for example. We have shown intuitively that
this
does not happen, but how can we
prove
it?
Returning to the
definition of rate of change between two points on a graph, separated by a
distance
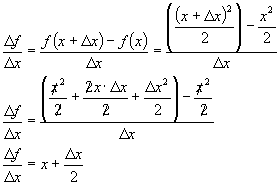
Notice that we are not
taking any limit as
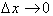 . The above equation holds true for any two points on the
graph of
. The above equation holds true for any two points on the
graph of
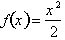 . Multiplying both sides by
. Multiplying both sides by
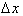 gives us:
gives us:
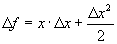
If we let
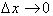 , then x is the derivative function such that:
, then x is the derivative function such that:
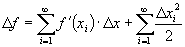
Therefore
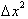 /2 represents the error associated with calculating
/2 represents the error associated with calculating
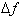 when we ignore it.
The total sum of errors from x = a to x = b, where
when we ignore it.
The total sum of errors from x = a to x = b, where
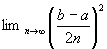 is:
is:
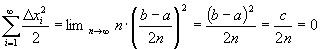
Thus the total error for
calculating the net change in
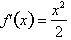 is:
is:
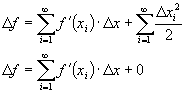
Remember that
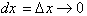 , therefore:
, therefore:
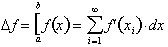
This important result
confirms the fact that the sum of the derivatives evaluated over infinite
times
over infinitely small intervals of dx from x = a to x = b corresponds
exactly
to the net change in the anti-derivative, f(x). We have proven this for
the
case of
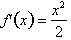 , but how do we prove it for the general case for any f(x)
and its derivative? More specifically we want to prove the following
fundamental theorem of Calculus.
, but how do we prove it for the general case for any f(x)
and its derivative? More specifically we want to prove the following
fundamental theorem of Calculus.
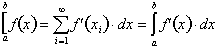
Here, the integral sign,
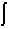 , replaces the summation sign,
, replaces the summation sign,
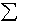 , and represents the infinite sum of the derivative evaluated
over an infinitely small interval, dx. To understand this let us take a
more
conceptual look at how the rate of change of a function is defined. The
following formula give us the average rate of change of f(x), through any
two
points on the graph of f(x).
, and represents the infinite sum of the derivative evaluated
over an infinitely small interval, dx. To understand this let us take a
more
conceptual look at how the rate of change of a function is defined. The
following formula give us the average rate of change of f(x), through any
two
points on the graph of f(x).
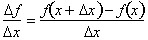
As we let
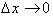 , the two points,
, the two points,
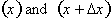 come closer together.
The average rate of change converges to the instantaneous rate of change of the function at that point, x.
come closer together.
The average rate of change converges to the instantaneous rate of change of the function at that point, x.
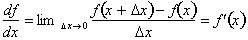
For any function,
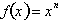 , as
, as
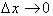 the rate of change
converges to a constant value over an infinitely small interval,
the rate of change
converges to a constant value over an infinitely small interval,
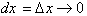 . Since the instantaneous rate of change, given by
. Since the instantaneous rate of change, given by
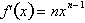 is constant over the
interval, dx, then an infinitely
small change in f(x), df, is found by
multiplying the definition of the derivative by dx, where
is constant over the
interval, dx, then an infinitely
small change in f(x), df, is found by
multiplying the definition of the derivative by dx, where
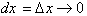
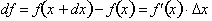
Thus the net change in
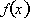 is the infinite sum
of the
is the infinite sum
of the
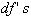 from x = a to x-b is:
from x = a to x-b is:
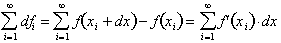
The first term
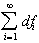 converges to
converges to
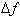 , while the second term,
, while the second term,
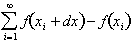 represents the net
change in the function,
represents the net
change in the function,
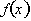 from x = a to x = b,
where
from x = a to x = b,
where
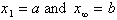 . Finally the last term is the infinite sum of the derivative
evaluate over each interval, dx. This
infinite sum is represented by the integral sign,
. Finally the last term is the infinite sum of the derivative
evaluate over each interval, dx. This
infinite sum is represented by the integral sign,
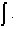
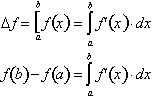
This the fundamental theorem of Calculus.
For example if f'(x)= 2x and we sum up 2xdx as
delta x goes to zero over an interval, we get the CHANGE in the anti-derivative function
F(x) over that same interval, where F(x) = x^2 .
Next section ->
Section 11.1 - Understanding Integration