CHAPTER 4
Chapter 4 - The Derivative
Section 4.2- Average Rate of Change
We have learned that a change in the
independent variable is defined as
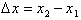, and the corresponding change in the dependent
variable over
this interval is
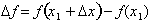The question we now must ask ourselves is how can we
measure the relative change of the dependent variable with respect to the
independent variable? In other words,
how do we calculate how much more or less
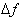changed compared to
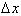
To calculate how much more
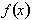changed over an interval from
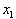
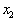, we simply divide the change in f over the change in x for
the interval. Thus we divide,
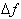by the interval over which we are evaluating it,
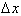which is equal to
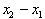. Thus the relative change of f with respect to x over an
interval
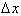is defined as:
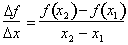
While this expression may seem
rather simple, it does require some explanation. By dividing the change in f by
the change in x what we are doing is calculating how much more f changed for a
given change in x. For example in the function,
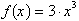, when x changed from 3 to 5, f changed from 81 to 375. Over
this interval of
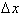from x=3 to x=5, the
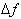was 294. Thus the
relative change in f with respect to a change in the independent variable x is:
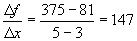
The value of 147 tells us that f
changes 147 times more than x over that
interval of
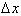from x=3 to x=5 only.
Thus for each unit change in x,
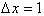, the corresponding change in f is 147. We can therefore
define the rate of change of a function with respect to its independent
variable to be:
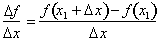
The value, called the rate of change of the function,
refers to how much more or less
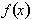changes for a unit
change in x. It is only valid over the interval under consideration,
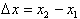
Another way of understanding what
rate of change of a function means is to look at the steepness of the line
connecting the two endpoints of the interval under consideration.
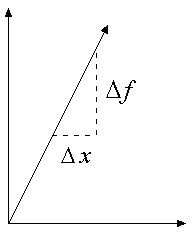
As
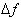increases, the
steepness of the line connecting the two endpoints will increase. Thus, the
greater the rate of change of the function, the greater its slope or steepness over the interval under consideration. Since slope and rate of
change are synonymous, then how is rate of change defined for functions whose graphs do not have constant slopes?
For example, from x=9 to x=12 of
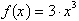, the change in f is 2997. Thus the rate of change of the
function over the interval is:
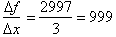
This value is
significantly higher than the rate of change calculated for the previous
interval from x = 3 to x = 5. We can only
conclude that the rate of change or slope of the graph must be
increasing and is not constant over an interval
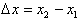. Look at the graph of the function
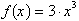to understand how this might be so:
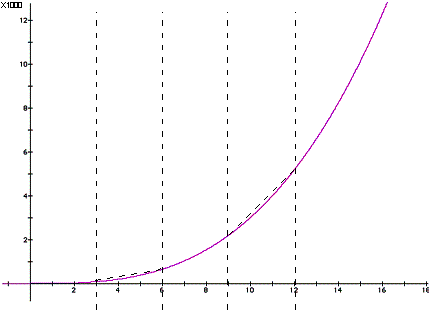
Since the rate of change of a function can change, then we have to come up with a
more refined definition of rate of change. We can define the average rate of
change of a function over an interval
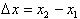, to be equal to
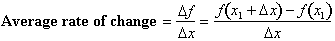
In the next
section we will take a closer look at how we can define the exact or instantaneous
rate of change of a function.
Next section ->
Section 4.3 - Instantaneous Rate of Change
