CHAPTER 6 - Applications of the Derivative
Chapter 6 - Applications of the Derivative
Section 6.2 - Instantaneous Velocity and Acceleration
When an object’s distance changes with time, its velocity
is the rate at which the distance is changing with respect to time, while its
acceleration is the rate at which the velocity is changing with respect to
time. As our time interval goes to zero, the velocity and acceleration of an
object take on instantaneous values at a certain moment. These instantaneous
rate of changes represent the derivatives
with respect to time.
To understand how the derivative relates to a moving
object, consider a Porsche that accelerates from
rest at a constant rate of 15 km/hr/s from a starting point d=0. It
continues at this acceleration until its velocity is 160 km/hr after which it
stops accelerating and maintains its velocity.
If we freeze the moment when 4 seconds have past then its
speedometer will read a velocity of exactly 60 km/hr at that instant only. However at t= 4.1 seconds the velocity
will be slightly higher since the car is accelerating.
This is why we use Calculus to analyze how these accelerations give rise to a
changing velocity that results in a changing distance that is covered.
The graph of its distance
from the starting point as a function of time is:
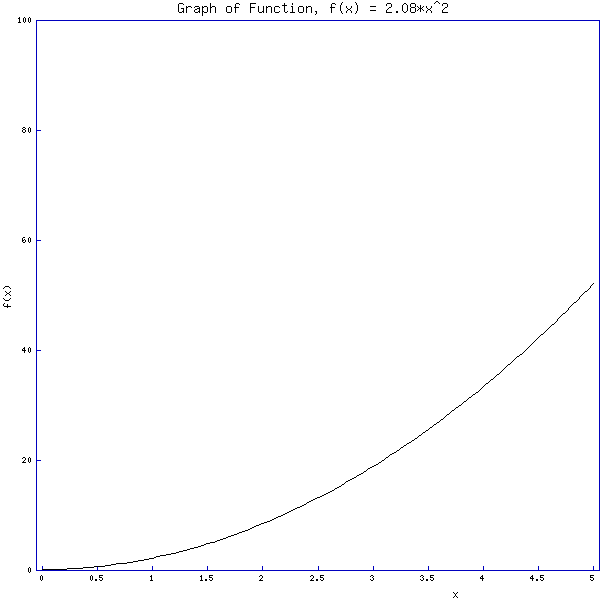
From the graph we can see that at t = 4 seconds the car
has covered 33 meters. Since the speedometer at that moment reads 60 km/hr, then we can say that at t= 4 seconds, its velocity is a constant 60 km/hr.
At t = 4.1
seconds, the velocity has
changed due to the car's acceleration. So the speedometer now reads 61 km/hr.
We can assume that from t= 4.0 seconds to t=4.1
seconds the velocity of the car is a constant 60 km/hr. By definition velocity
is the distance covered divide by the time taken to cover the distance or
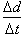Thus, the distance covered by the car in this
small time interval, divided by the time, .1 seconds, will give us 60 km/hr.
Since the velocity of the car is increasing, due to its constant rate of acceleration, the velocity of the Porsche at any instant,
t, will be whatever the speedometer
reads at that moment.
If we were given the relationship for distance covered as
a function of time t, then velocity of the car at any time t can be found by
calculating the distance covered
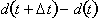over a time interval,
:
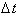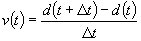
Since the car is accelerating,
its velocity is not constant over the
interval
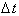. We can assume the velocity is constant over an infinitely
small time interval,
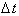
Therefore
we have to take the limit as
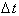goes to zero to find
the instantaneous rate of change of
distance with respect to time. The instantaneous rate of change of distance
will correspond exactly to what the speedometer reads at time t.
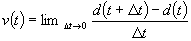
From the definition of the
derivative:
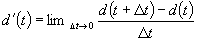
This leads to the extremely
important result:
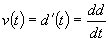
The velocity at any time t is the instantaneous rate of
change of the distance function at a time t. By definition the derivative is
the instantaneous rate of change of a function over an infinitely small
interval. thus the derivative of the distance function,
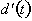with respect to time is the
velocity function for the object
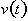
We now need to derive an expression for acceleration as
function of time. In the same way that velocity is the rate of change of
distance with respect to time, acceleration is the rate of change of velocity
with respect to time.
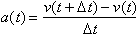
To find the instantaneous
acceleration at any time t, we need to take the limit as
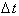goes to zero. Without
taking the limit,
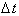is a discrete value such that the calculated
acceleration is the average acceleration is for that interval. By taking the
limit as
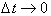, we are assuming the acceleration is constant over that time
interval.
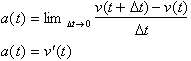
This proves that acceleration is the derivative of the velocity function with respect to time. Since
velocity is the first derivative of
the distance function with respect to time, the acceleration function is the second derivative of the distance
function. In other words the acceleration function is obtained by
differentiating the distance function twice. Our results can be summarized as
follows:
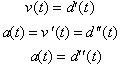
Next section ->
Section 7.1 - What is a Force?
